АГС-12/0,6 (АГС 12/2) | Автономные системы пожаротушения с тепловым пуском от «НПГ Гранит-Саламандра»
Тех. характеристики|
Масса устройства, кг |
0,18 |
|
Масса аэрозолеобразующего заряда, кг |
0,03 |
|
Огнетушащая способность аэрозоля, кг/м3 |
0,05 |
|
Максимальный защищаемый объем условно герметичного помещения (δ* < 0,001м-1), м3 |
0,6 |
|
Размер Генератора с креплением ( Ш х Д х В ), мм |
105 х 105 x 35 |
|
Направление аэрозольного потока |
Радиальное (360гр.) |
|
Время работы, с |
8 |
|
Классы тушения пожаров |
*δ — отношение суммарной площади постоянно открытых проемов к объему защищаемого помещения
Принцип действияПринцип действия
При подаче теплового импульса на узел запуска происходит воспламенение шашки аэрозолеобразующего состава, при сгорании которого образуется пожаротушащая газоаэрозольная смесь, состоящая из мелкодисперсных твердых частиц (около 70% от всей массы исходного состава) и газа, поступающего в защищаемый объем.
Подготовка устройства к работе
Автономное устройство огнетушащего аэрозоля серии АГС 12/0,6 с тепловым пуском устанавливается на ограждающих конструкциях.
Крепление осуществляется с помощью различного типа метизов через два отверстия диаметром 3 мм или на двусторонний скотч.
| Обезжирить поверхность | |
| Снять защитную пленку с тыльной стороны устройства серии АГС 12/0,6 | |
| Плотно прижать к поверхности | |
| Возможно крепление с помощью метизов |
Установку устройства серии АГС 12/0,6 на скотч проводить в отапливаемом помещении, при нормальных климатических условиях, после чего в месте установки устройства температурный режим не должен меняться в течение 3-х часов.
Ежегодно неисправные электроустановки провоцируют около 40 000 пожаров в масштабах страны, причем есть тенденция к росту — только за последнюю пятилетку количество таких возгораний увеличилось на 17%.
Пожарная безопасность детских дошкольных и образовательных учрежденийЗдания, где пребывают дети, требуют особого подхода к противопожарной защите. Пожарная безопасность в образовательных учреждениях и детских садах предполагает целый комплекс мероприятий — от автоматической системы огнетушения до спецобработки эвакуационных путей (огнезащитные краски и покрытия). В случае ЧС важно не допустить распространения пламени. Для этого в потенциально опасных местах, таких как щитки и прочие электроустановки, целесообразно использовать автономные огнетушители, например, аэрозольные генераторы.
По действующим нормативам пожарная безопасность жилых зданий высотой от 28 метров должна быть повсеместной, но и в постройках малой этажности целесообразно максимально защитить людей и имущество от огня.
Установки аэрозольного пожаротушенияСреди наиболее эффективных огнетушащих материалов выделяют аэрозоль. Облако из твердых мелкодисперсных частиц обладает высокой проникающей способностью, быстро заполняет весь объем помещения и угнетает реакции горения.
Автономные установки пожаротушения: сравниваем аэрозольные и газовые системы К самым эффективным методам активной огнезащиты относятся автономные системы пожаротушения. Они самостоятельно обнаруживают возгорание и тушат пламя даже при отсутствии источников энергоснабжения и внешних систем управления. Автономное пожаротушение не следует путать с автоматическим, так как системы-автоматы нуждаются в электропитании и срабатывают при поступлении соответствующей команды с управляющей аппаратуры. Пожарная безопасность электроустановокВ настоящее время проблема пожарной безопасности электроустановок в России приобретает все большую актуальность. Это обусловлено пугающим ростом количества пожаров по данным статистики разных регионов. Доля пожаров, происходящих по электротехническим причинам, за последнюю пятилетку увеличилась в среднем на 17%.
Это обусловлено пугающим ростом количества пожаров по данным статистики разных регионов. Доля пожаров, происходящих по электротехническим причинам, за последнюю пятилетку увеличилась в среднем на 17%.
Практически вся информация хранится сейчас в электронном виде. Этот способ гораздо удобнее бумажных архивов, однако новые технологии связаны с новыми факторами риска.
|
Блок источника резервированного питания БИРП12/6,0 обеспечивает выходную мощность до 72 Вт в сетевом диапазоне от 150 до 265В благодаря применению импульсного ШИМ-преобразователя. Электронная схема прибора обеспечивает стабилизированное выходное напряжение и защищает нагрузку от импульсов и всплесков сетевого напряжения и иных отклонений от нормальных параметров работы электросети, что позволяет использовать его для питания таких систем как: Системы охранно-пожарной сигнализации которые могут включать сетевые контроллеры, преобразователи интерфейсов, блоки индикации и управления, релейные блоки, приёмно-контрольные приборы, охранные извещатели, блоки управления пожарным оповещением, приборы речевого оповещения, световые и звуковые оповещатели, световые табло, приборы управления пожаротушением, насосными станциями, контроллеры адресной линии, адресные расширители, адресные релейные блоки, пожарные извещатели. Системы контроля и управления доступом: Сетевые дверные, лифтовые, шлюзовые контроллеры доступа, считыватели, релейные блоки, эл/м замки.
|
При отключении сетевого напряжения БИРП-12/6,0 обеспечивает питание нагрузки от резервного источника электропитания – аккумуляторной батареи. Продолжительность автономной работы от аккумуляторной батареи 24 (12+12)Ач при номинальной выходной мощности составляет 4 часа. Независимый канал заряда мощностью 10Вт обеспечивает восстановление ресурса аккумуляторной батареи за 36 часов. Также БИРП-12/6,0 обеспечивает выдачу информационных диагностических сообщений с помощью световых индикаторов и имеет информационные выходы «Контроль Сети (КС)», «Контроль батареи (КБ)» и «Контроль выхода (КВ)» и Датчик вскрытия корпуса («Тампер ) для передачи информации во внешние цепи, что соответствует требованиям технического регламент о требованиях пожарной безопасности (ФЗ- №123). |
С-реактивный белок человека ультрачувствительный (CRP) – Bialexa
Описание и функции С-реактивного белка (CRP)
С-реактивный белок (СРБ) был впервые обнаружен исследователями Тиллетт и Францис в 1930 году в качестве элемента сыворотки крови больных с острыми воспалительными процессами, вступающего в реакцию с C-полисахаридом пневмококка. СРБ человека принадлежит к очень консервативной семье белков под названием «пентраксины», которая характеризуется наличием кальций-зависимого связывания лигандов и радиальной симметрией пяти мономеров, образующих кольцо вокруг центральной поры. Молекула СРБ состоит из 224 остатков аминокислот с молекулярной массой мономера порядка 25 кДа и pI 6,4. Мономеры нековалентно связаны и образуют пентамерную структуру (Рис. 1).
В течение многих десятилетий СРБ был известен в качестве белка, синтезируемого в печени. Тем не менее, последние исследования свидетельствуют о существенном уровне экспрессии СРБ в других тканях, в том числе в стенках кровеносных сосудов и в гладкомышечных клетках коронарных артерий, где, согласно предположениям ученых, СРБ представлен в виде мономера (mCRP), в то время как нативный пентамерный белок (nCRP) содержится преимущественно в плазме.
Точная функция СРБ в организме человека до сих пор вызывает многочисленные дискуссии. Было установлено, что указанный белок принимает участие в воспалительных, а также во врожденных иммунологических процессах организма. Важными элементами биологической активности СРБ являются его способность с высоким уровнем аффинности связывать различные лиганды, в том числе поврежденные клеточные мембраны, апоптотические клетки, фибронектин и т.
Рис. 1. Структура С–реактивного белка.
Использование С-реактивного белка на практике
В клинической практике С-реактивный белок рассматривается в качестве основного, хотя и достаточно неспецифичного, маркера воспаления. Он относится к так называемым «белкам острой фазы» (БОФ), которые появляются в крови в ответ на какое-либо повреждение тканей организма, вызванное инфекцией, воспалением, опухолевым ростом, травмой и другими факторами. СРБ классифицируют как белок «сильной» подгруппы: его содержание в крови может повышаться в тысячи раз, в отличие от слабых БОФ. Кроме того, время появления С-реактивного белка составляет от 6 до 12 часов, тогда как белки слабой подгруппы можно определить в крови только через 48-72 часа. Это делает его чрезвычайно эффективным маркером, если говорить о времени выявления патологий.
Как правило, у относительно здоровых людей, содержание СРБ составляет менее 5 мг/л. При наличии патологий концентрация СРБ может находиться в пределах огромного, 10000-кратного диапазона (примерно 0,05-500 мг/л). Различают несколько уровней его содержания в крови:
- отрицательный — до 3,0 мг/л,
- C-реактивный белок слабоположительный — 3,0 — 6,0 мг/л,
- положительный — 6,0 — 12,0 мг/л,
- СРБ резко положительный — от 12,0 мг/л и выше.
Самые высокие уровни содержания СРБ (выше 30 мг/л) наблюдаются при наличии бактериальных инфекций, таких как септический артрит, менингит и пневмония. При вирусных инфекциях уровень белка гораздо ниже, что позволяет использовать количественный анализ для дифференциации этих двух инфекций. Умеренно высокая концентрация СРБ, примерно 10-40 мг/л, была обнаружена у пациентов, перенесших инфаркт миокарда и страдающих от иных повреждений тканей.
C-реактивный белок (CRP) используется для диагностики воспалений наряду с таким показателем, как СОЭ (скорость оседания эритроцитов). Однако исследование CRP позволяет установить воспаление раньше, так как его уровень повышается прежде, чем изменяется СОЭ.
Рост содержания СРБ (с-реактивного белка) в крови наблюдается не только при воспалениях бактериального и вирусного происхождения, но и при любых повреждениях тканей, в том числе некрозах, опухолях, паразитарных инфекциях, что существенно расширяет его использование в диагностике. Кроме того, благодаря широкому диапазону значений, и корреляции с показателем СОЭ можно провести сравнительно точную дифференциацию типа заболевания.
В 2003 году Центр по контролю и профилактике заболеваний США (CDC) и Американская ассоциация кардиологов (AHA) выступили с заявлением, в котором признали СРБ наиболее эффективным маркером воспаления, рекомендованным к использованию в современной клинической практике для оценки сердечно-сосудистых рисков. Многочисленные эпидемиологические исследования показали, что СРБ является сильным независимым предиктором развития сердечно-сосудистых осложнений, в том числе инфаркта миокарда, ишемического инсульта, заболевания периферических сосудов и внезапной сердечной смерти в отсутствии известных сердечно-сосудистых заболеваний (согласно обзору «Clearfield»).
Рекомендации Центра по контролю и профилактике заболеваний США и Американской ассоциации кардиологов предписывают использование СРБ для первичной профилактики и установления предельных пороговых точек в соответствии с категориями относительно риска: низкий риск (<1,0 мг/л), средний риск (1,0-3,0 мг/л), и высокий риск (> 3,0 мг/л). В связи с этим используемые в настоящее время высокочувствительные методы измерения концентрации СРБ (hsCRP) позволяют определить его содержание, измеряемое нанограммами на миллилитр (нг/мл). Аббревиатура hsCRP (high sensitivity CRP, C-реактивный белок ультрачувствительный) получила всеобщее признание и повсеместное распространение для обозначения белка, обнаруженного в результате таких исследований. Исследователи пришли к выводу о наличии существенной взаимосвязи между содержанием hsCRP в плазме крови и риском смерти у пациентов с острым коронарным синдромом. Кроме того, Кёниг и соавторы утверждают, что повышенная концентрация циркулирующего hsCRP свидетельствует о высоком риске смерти от ряда распространенных хронических заболеваний.
Исследователи пришли к выводу о наличии существенной взаимосвязи между содержанием hsCRP в плазме крови и риском смерти у пациентов с острым коронарным синдромом. Кроме того, Кёниг и соавторы утверждают, что повышенная концентрация циркулирующего hsCRP свидетельствует о высоком риске смерти от ряда распространенных хронических заболеваний.
Моноклональные антитела к CRP компании Биалекса
Новейший количественный иммуноферментный анализ с использованием уникальных произведенных компанией Биалекса моноклональных антител характеризуется высоким уровнем чувствительности и имеет линейный диапазон детектирования в пределах от 0,025 мг/л до 2,5 мг/л при проведении магнитного биосенсорного анализа; от 0,01 мг/л до 50 мг/л при проведении количественного иммунохемилюминесцентного анализа (в обоих типах исследований предел обнаружения составляет 0,004 мг/л). При проведении сэндвич ELISA с использованием нанокристаллов был достигнут предел обнаружения 0,0011 мг/л. Обнаруженные нами наиболее эффективные пары моноклональных антител (4С6 — 5Е9 и 5B8 — 3C5, а также некоторые другие) обладают 10000-кратным диапазоном линейности при проведении экспериментальных ИФА. Комбинации указанных антител могут использоваться для проведения hsCRP-исследований на базе различных диагностических платформ. В традиционных СРБ-исследованиях зачастую используются методы турбидиметрии и конкурентного анализа, для которых предпочтительным считается применение моноклональных антител с относительно низкой аффинностью. Для удобства наших клиентов мы разработали моноклональные антитела с различным уровнем аффинности, что позволяет использовать такие антитела для проведения различных типов иммунологических исследований.
В молекуле нативного СРБ каждый протомер скоординирован двумя ионами Ca2+. Компания Биалекса предлагает моноклональные антитела к СРБ как чувствительные, так и нечувствительные к отсутствию Ca2+ в растворе. Некоторые антитела распознают антигены только в присутствии ионов Ca2+ (моноклональные антитела 3B6, 4B7). Большинство предлагаемых компанией Биалекса моноклональных антител нечувствительны к присутствию ионов Ca2+ при проведении иммунологических исследований сэндвич-методом и способны эффективно распознавать антигены даже при наличии ЭДТА в исследуемом образце (моноклональные антитела 11E12, 4C6, 5B8, 5E9, 5H6, 1C1, 3C10, 3С6, 10C3, 3C5, 16С9). Все моноклональные антитела к СРБ компании Биалекса прошли испытания в рамках различных иммунологических применений.
Большинство предлагаемых компанией Биалекса моноклональных антител нечувствительны к присутствию ионов Ca2+ при проведении иммунологических исследований сэндвич-методом и способны эффективно распознавать антигены даже при наличии ЭДТА в исследуемом образце (моноклональные антитела 11E12, 4C6, 5B8, 5E9, 5H6, 1C1, 3C10, 3С6, 10C3, 3C5, 16С9). Все моноклональные антитела к СРБ компании Биалекса прошли испытания в рамках различных иммунологических применений.
Также компания Биалекса предлагает нативный C-реактивный белок для инвитро-диагностики, иммунологических и биохимических исследований, с чистотой более 95% (по результатам ДСН-электрофореза). СРБ используется в качестве стандарта для иммуноанализа, а также как антиген для получения сыворотки, содержащей соответствующие антитела и применяемой в дальнейших исследованиях.
Цена на C-реактивный белок оговаривается индивидуально, для уточнения позвоните по номеру, указанному на сайте.
Моноклональные антитела к С-реактивному белкуС-реактивный белок (CRP)
Similac (Abbott) Гипоаллергенный 1 (0-6 месяцев) 400 г
Самые выгодные предложения по Similac (Abbott) Гипоаллергенный 1 (0-6 месяцев) 400 г
Svetlana, 10.06.2019
Достоинства:
Малое содержание лактозы не вызывает проблем при непереносимости, но улучшает пищеварение по сравнению с совсем безлактозной смесью. Нормально разводится.
Недостатки:
Ложка закопана в смесь, не удобная.
Тамара Григоренко, 12.04.2019
Достоинства:
Удобная тара и мерная ложечка, банку можно потом использовать в домашнем быту. Действительно смесь для аллергиков с пищевой аллергией полезна.
Действительно смесь для аллергиков с пищевой аллергией полезна.
Недостатки:
Запах и вкус не очень приятные.
Комментарий:
Моему малышу сейчас уже 1 год 9 мес, с рождения у нас пошла аллергия на молочный белок и яичный, врачи советовали несколько видов смеси мы их все попробовали, но остановились на Смеси Similac Гиппоаллергенный 1 и 2, он более подошел по восприятию его ребенком, реакция на коже заметно улучшилась. Стало меньше высыпаний, единственное что не понравилось так это вкус смеси и запах, как будто разные таблетки смешали в молоке. Но лекарство и не должно быть вкусным, главное что смесь полезна деткам с аллергией на белок.
Вера, 20.03.2019
Достоинства:
можно хранить в холодильнике готовую смесь
Недостатки:
ложка большая и в самой в смеси лежии,не удобная дозировка ложки.комки.
Комментарий:
назначали в качестве лечения.очень не довольна всей линейкой этой фирмы.если у вас нет другой ложки,то вам придется лазить руками и искать ее в банке на дне.эта ложка рассчитана на 60мл,а мой ребенок пьет по 30мл.постоянно приходится отливать.комочки-это нечто!!!хоть в пену взбивай-они останутся!постоянно забивается соска.Это 7 смесь,которую мы пробуем,поэтому нам есть с чем сравнить.симптомы аллергии не ушли,а даже усилились.
Гость, 14.03.2019
Достоинства:
Спас в период аллергии, не вызывает колик
Недостатки:
Ужасный запах
Плохо растворяется по сравнению с другими смесях и, прям кусочки, которые приходится разбивать и размешивать, иногда даже соска забивается
Для постоянного применения дорого,впрочем как большинство смесей в банке
Гость, 11. 03.2019
03.2019
Достоинства:
Смесь специально для детей с аллергией. В баночке присутствует удобная мерная ложечка.
Недостатки:
Более высокая цена по сравнению с обычными смесями
Комментарий:
У детей была аллергия (красные пятна на кожи) на обычные смеси всех производителей и только эта смесь им подошла.
Инна Усоева, 06.03.2019
Достоинства:
Действительно не вызывает аллергии, уменьшает симптомы её появления, небольшое количества лактозы, живот перестал болеть
Недостатки:
Мерная ложка, большая, приходится использовать от другой смеси
Комментарий:
Смесь нормальная, разбодим её в стакане, после чего переживаем в бутылочку, тем самым уменьшаем образование колик у ребёнка. В холодной воде, даже комнатной температуры, развести смесь нереально, при допустимых градусах 37-40 все идеально. После применения у ребёнка исчезло акне.
Timmy Ganiev, 01.03.2019
Достоинства:
Оперативность подтверждения заказа, доставка без существенной задержки
Добрынина Таня, 08.02.2019
Достоинства:
без пальмового масла,без лактозы,быстро растворяется
Комментарий:
Смесь хорошая на вкус, нам подошол, больше нет алергии коликов и запоров.-reshenie-1408.jpg)
petrovicheva.da, 15.02.2018
Достоинства:
Хороший состав
Недостатки:
Цена
Комментарий:
Моему ребёнку смесь подошла, ни запоров, ни плохого стула или срыгиваний нет. Первый раз не хотел её есть, но быстро привык и спустя месяц он аж трудится от нетерпения когда подношу бутылку. А цена- я считаю на питании младенца экономить точно нельзя!
Мария, 28.05.2017
Достоинства:
Нет аллергии на коже, ребёнку нравится
Недостатки:
Нет в продаже экономной большой упаковки
Комментарий:
После того, как у ребёнка появилась аллергия на коже, стали пользоваться гипоаллергенной смесью. Ребёнку по началу было не привычно, но сейчас за уши не оттащить. Очень нравится. На коже никакой аллергии.
Гость, 17.02.2017
Достоинства:
Удобная фасовка, знаменитый бренд, без лактозы
Недостатки:
Разве что цена
Комментарий:
Пробовали разные смеси, но только от этой животик у малыша не болит. Видимо оттого, что без лактозы.
светлана, 15.10.2016
Достоинства:
у ребенка уменьшился диатез
Недостатки:
цена поднялась . .брала дешевле
.брала дешевле
Комментарий:
хорошо бы если смесь выпускали больших более экономичных упаковках
Products | Friso Russia
Friso Gold 1Сухая адаптированная начальная молочная смесь.
Где купить Friso Gold 2Сухая адаптированная последующая молочная смесь.
Где купить Friso Gold 3Сухой молочный напиток.
Где купить FRISO 1“Фрисо 1 LockNutri” (“Friso 1 LockNutri”) — продукт детского питания для детей раннего возраста, смесь молочная сухая начальная адаптированная для смешанного и искусственного вскармливания детей с рождения до 6 месяцев. Смесь содержит важные питательные вещества для здорового роста и развития вашего малыша.
Фрисо 2 LockNutri” (“Friso 2 LockNutri”) – продукт детского питания для детей раннего возраста, смесь молочная cухая адаптированная последующая для смешанного и искусственного вскармливания детей с 6 до 12 месяцев.
Где купить FRISO 3“Фрисо 3 LockNutri” (“Friso 3 LockNutri”) – продукт детского питания для детей раннего возраста, напиток молочный сухой для детей старше 12 месяцев.
Где купить Friso VOM 1 ComfortСухая молочная смесь для детей со срыгиваниями, запорами и коликами.
Где купить Friso VOM 2 ComfortСмесь содержит камедь рожкового дерева, природный загуститель, для устранения нарушений пищеварения у детей.
Для детей с риском развития пищевой аллергии
Где купить Friso Гипоаллергенный 2Смесь содержит частично гидролизованный белок, снижающий риск развития аллергии к белкам коровьего молока.
Где купить Friso PEPСпециальная формула для диетического (лечебного) питания детей с аллергией к белкам коровьего молока.
Где купить Friso PEP ACСпециальная формула для диетического (лечебного) питания детей с аллергией к белкам коровьего молока.
Где купитьАзбука Friso
Незнакомый термин? Незнакомый ингредиент в составе? Азбука Friso поможет разобраться в незнакомых терминах. Узнать больше
Узнать большеНШВИ 6.0-12, Наконечник штыревой втулочный изолированный желтый 6.0 мм кв.
Описание
Наконечники НШВИ предназначены для оконцевания методом опрессовки гибких многопроволочных медных проводников. Они трансформируют концы многожильных проводов в монолитные штифты.
Наконечники НШВИ являются удобной альтернативой обязательному облуживанию концов многожильных проводников при подсоединении к клеммам.
Для монтажа одного провода
Предназначены для оконцевания методом опрессовки гибких многопроволочных медных проводников. Трансформируют концы многожильных проводов в монолитные штифты
Современная альтернатива обязательному облуживанию концов многожильных проводников при подсоединении к клеммам
Максимальное напряжение: 690 В
Размеры изолированных манжет и втулок наконечников НШВИ рассчитаны для монтажа одного проводника соответствующего сечения
Материал коннектора: медь марки М1
Покрытие коннектора: электролитическое лужение
Материал изоляции: полипропилен. Не содержит галогенов
Термостойкость изоляции: 105оC
Цвет изолирующих манжет выполнен в соответствии с цветовой маркировкой DIN 46228, часть 4
Одинарные и двойные втулочные наконечники «КВТ» представлены в одинаковой цветовой гамме стандарта DIN, что облегчает их поразмерную идентификацию
Коническая форма манжеты, тип «Easy Entry», облегчает заведение многожильного провода внутрь медной втулки
Обжим провода поверх медной втулки
ТУ 3424-001-59861269-2004
Технические параметры
| Тип используемого кабеля | один провод |
| Длина контактной части, мм | 12 |
| Функциональное назначение | наконечник втулочный |
| Серия | ншви |
| Максимальное сечение зажимаемого провода,кв.мм | 6 |
| Цвет изолятора | желтый |
| Наличие изоляции | есть |
| Вес, г | 0. 5 5 |
Техническая документация
Инфляция в России продолжает замедляться
Инфляция в России с 6 по 12 апреля снизилась до 0,1% после трех недель нахождения показателя на отметке 0,2%, свидетельствуют данные Росстата.
Исходя из среднесуточной динамики показателя, годовая инфляция к 12 апреля замедлилась до 5,55% с уровня 5,66%, достигнутого неделей ранее. Таким образом, продолжается снижение инфляции с пятилетнего пика, достигнутого в марте на отметке 5,8%.
С начала года к 12 апреля потребительские цены выросли на 2,3%, с начала месяца — на 0,2%. Средняя стоимость автомобильного бензина и дизельного топлива за отчетный период повысились на 0,1%.
В середине марта Банк России на очередном заседании неожиданно повысил ключевую ставку на 0,25 п. п. впервые с конца 2018 г. Комментируя это решение, регулятор отметил, что темп роста потребительских цен в I квартале складывается выше прогноза ЦБ.
Восстановление внутреннего спроса приобретает устойчивость и происходит быстрее, чем ожидалось ранее, в ряде секторов опережая темпы наращивания выпуска. Инфляционные ожидания населения и бизнеса остаются на повышенном уровне. Баланс рисков сместился в сторону проинфляционных.
Быстрое восстановление спроса и повышенное инфляционное давление формируют необходимость возвращения к нейтральной денежно-кредитной политике. Сроки и темпы этого процесса Банк России продолжит определять с учетом фактической и ожидаемой динамики инфляции относительно цели, развития экономики на прогнозном горизонте, а также оценивая риски со стороны внутренних и внешних условий и реакции на них финансовых рынков.
При этом ЦБ допускает возможность дальнейшего повышения ключевой ставки на ближайших заседаниях. По прогнозу Банка России, с учетом проводимой денежно-кредитной политики годовая инфляция вернется к цели регулятора вблизи 4% в первой половине 2022 г. и будет находиться на этом уровне в дальнейшем.
Минэкономразвития ожидает замедление годовой инфляции в апреле до 5,5-5,6% с пиковых 5,8% в марте. В опубликованном на прошлой неделе мониторинге министерства «Картина инфляции» отмечается, что в марте пройден пик годовой инфляции. Начиная с апреля ожидается ее замедление в условиях выхода из расчета низкой базы начала прошлого года. По итогам апреля инфляция в помесячном выражении, по оценке, составит 0,5-0,6%, что соответствует диапазону 5,5-5,6% в годовом выражении.
БКС Мир инвестиций
Этикетки для удобрений: что означают числа N-P-K
Красивые газоны и сады начинаются со здоровых, хорошо ухоженных растений. Потребности каждого растения, от трав до цветущих кустарников, различаются, но некоторые основы применимы ко всем. Выбор подходящих удобрений для вашего газона и сада не должен быть трудным. Вооружившись основами удобрений, сделать правильный выбор так же просто, как 1-2-3:
.Все удобрения должны содержать единообразную информацию, чтобы потребители могли легко сравнивать товары.На каждой этикетке есть три заметных числа, обычно прямо над или под названием продукта. Эти три числа образуют то, что называется соотношением N-P-K удобрения — пропорцией трех питательных веществ для растений по порядку: азота (N), фосфора (P) и калия (K).
Числа N-P-K продукта отражают процентное содержание каждого питательного вещества по массе. Например, на этикетке 12-фунтового мешка Pennington Ultragreen Lawn Fertilizer 30-0-4 указано, что оно содержит 30 процентов азота, 0 процентов фосфора и 4 процента калия, помимо других полезных ингредиентов.Это удобно, когда результаты анализа почвы рекомендуют количество фактического азота в фунтах, а не конкретные удобрения. Умножив 12 фунтов на 0,30, вы увидите, что этот 12-фунтовый мешок содержит чуть больше 3,6 фунтов азота.
Пышные травы цветут благодаря удобрениям с высоким содержанием азота.
Растения нуждаются в большем количестве азота, фосфора и калия, чем любые другие питательные вещества для растений. Эти три вещества, часто называемые первичными макроэлементами, входят в число 17 питательных веществ, необходимых для всей жизни растений.Другие элементы, такие как железо, не менее важны для выживания растений, но растениям они нужны в гораздо меньших количествах. Кроме того, у разных растений разные потребности. Например, азалии нужно больше железа, чем многим другим растениям, поэтому специальные удобрения, такие как Lilly Miller Rhododendron, Evergreen & Azalea Food 10-5-4, содержат дополнительное количество железа. Это количество железа указано на панели ингредиентов на этикетке продукта, но не в соотношении N-P-K.
Эти три вещества, часто называемые первичными макроэлементами, входят в число 17 питательных веществ, необходимых для всей жизни растений.Другие элементы, такие как железо, не менее важны для выживания растений, но растениям они нужны в гораздо меньших количествах. Кроме того, у разных растений разные потребности. Например, азалии нужно больше железа, чем многим другим растениям, поэтому специальные удобрения, такие как Lilly Miller Rhododendron, Evergreen & Azalea Food 10-5-4, содержат дополнительное количество железа. Это количество железа указано на панели ингредиентов на этикетке продукта, но не в соотношении N-P-K.
Растения получают все необходимые питательные вещества естественным образом из воздуха и почвы, но почва может истощаться, особенно в цветущих лужайках и садах.Поскольку растения используют большее количество N-P-K, эти питательные вещества нуждаются в частом пополнении. Есть и другие факторы. Азот свободно перемещается в почве, поэтому вода из-за проливных дождей или ирригации крадет азот в процессе, называемом выщелачиванием. Удобрения вступают в действие и восполняют использованные и потерянные питательные вещества, чтобы газоны и сады оставались ухоженными.
Удобрения из азалии содержат дополнительное железо для здоровых кустов.
Каждое из трех питательных веществ в N-P-K выполняет свою особую работу.Азот (N) стимулирует энергичный рост листвы и насыщенный зеленый цвет газонных трав и других растений. Без достаточного количества азота рост замедляется, а газоны и растения бледнеют. Из-за слишком большого количества азота цветущие и плодоносящие растения прилагают усилия к зеленому росту и теряют цветение и плоды.
Фосфор (P) направляет энергию на сильное развитие корней и цветов, фруктов и семян, а также помогает растениям эффективно использовать другие питательные вещества. Недостаток фосфора приводит к ослаблению корней и недостатку цветов и плодов . Все больше штатов и округов ограничивают внесение фосфора на газоны из-за экологических проблем, связанных со стоком фосфора в водные пути. В этих штатах или округах домовладельцы обычно могут применять стартовые удобрения для газонов с высоким содержанием фосфора, такие как Pennington UltraGreen Starter Fertilizer 22-23-4, если анализ почвы показывает дефицит питательных веществ. Проконсультируйтесь с агентом по оказанию помощи в вашем округе, чтобы узнать об ограничениях в применении питательных веществ.
В этих штатах или округах домовладельцы обычно могут применять стартовые удобрения для газонов с высоким содержанием фосфора, такие как Pennington UltraGreen Starter Fertilizer 22-23-4, если анализ почвы показывает дефицит питательных веществ. Проконсультируйтесь с агентом по оказанию помощи в вашем округе, чтобы узнать об ограничениях в применении питательных веществ.
Калий (K) ускоряет общий рост.Он помогает регулировать рост корней и верхушек, а также сохраняет растения здоровыми и сбалансированными. Это влияет на все аспекты благополучия газона и сада, от устойчивости к холоду и засухе до устойчивости к болезням и вредителям.
Дополнительный фосфор и калий поддерживают большие сочные помидоры.
Красивый газон нуждается в интенсивном росте и насыщенном цвете, обильном поступлении азота, поэтому удобрения для газонов имеют соотношение N-P-K, причем первое число намного выше, чем два других. Почва обычно обеспечивает достаточное количество фосфора и большую часть калия, в котором нуждается здоровая трава, поэтому количество этих питательных веществ невелико.
Вкусным помидорам и другим овощам тоже нужен азот, но для цветения и сбора урожая требуется больше фосфора и калия. Вот почему второе и третье числа больше всего у таких продуктов, как Lilly Miller MORCROP Tomato & Vegetable Food 5-10-10.
Здоровые корни цветущих луковиц зависят от фосфора, поэтому удобрения для луковиц, в том числе Lilly Miller Bone Meal 6-12-0, имеют высокое среднее число. Универсальные удобрения, такие как Lilly Miller All Purpose Planting and Growing Food 10-10-10, обеспечивают сбалансированный N-P-K, разработанный для всестороннего здоровья сада.
Понимая основы этикеток на удобрениях, вы можете с уверенностью выбирать продукты, подходящие для ваших газонов и садов. Ассортимент удобрений для газонов и сада Pennington может помочь вашему газону и саду полностью раскрыть свой потенциал красоты и удовольствия.
Лучшие варианты удобрений для газона для вашего двора (Руководство покупателя)
Фото: istockphoto. com
com
Кто бы ни сказал: «С другой стороны трава всегда зеленее», вероятно, использовал неправильный материал.Когда дело доходит до содержания двора в идеальном состоянии, все, что вам действительно нужно, — это лучшие удобрения для газонов для вашего климата и условий, а также несколько дат, обведенных в календаре. После того, как вы определились с идеалом, просто подайте заявку в соответствии с инструкциями и выполните действия в соответствии с инструкциями на упаковке. Это руководство научит вас основам удобрений и предложит обзоры некоторых продуктов с самым высоким рейтингом на рынке.
- ЛУЧШЕЕ В ЦЕЛОМ: Milorganite Garden Care Organic Fertilizer
- ECO PICK: Более безопасное удобрение для восстановления газонов
- ТАКЖЕ УЧИТЫВАЙТЕ: Scotts Liquid Turf Builder Корм для газонов
Основные соображения при выборе удобрения для газонов
Разберитесь в цифрах.Вы, несомненно, заметили три цифры, напечатанные на этикетках удобрений для газонов. Число, известное как соотношение NPK, обозначает процент основных питательных веществ (N для азота, P для фосфора, K для калия), содержащихся в удобрении. Если, например, соотношение NPK в удобрении составляет 12-0-10, оно содержит 12 процентов азота, отсутствие фосфора и 10 процентов калия.
Вообще говоря, азот помогает растениям оставаться зелеными, фосфор способствует росту корней (хотя это может вызывать споры из-за его склонности к загрязнению воды), а калий защищает от засухи и болезней.В зависимости от типа газона и климата, в котором вы живете, одна комбинация будет лучше, чем другие. Сравните упаковку с вашими видами травы, чтобы убедиться, что в ней есть оптимальный баланс питательных веществ для ваших конкретных потребностей.
Выберите свой тип. После того, как вы определите наилучшее количество NPK, пора выбрать между синтетическим или органическим удобрением. Синтетические разновидности создаются из минералов, газов и даже отходов с целью получения быстрых результатов — иногда в течение нескольких дней.Недостатком синтетических удобрений является их репутация «сжигающих» (т. Е. Убивающих) траву, если они используются слишком жестоко. Они также могут нанести вред окружающей среде и нанести вред здоровью, если они попадут в местный водопровод.
Синтетические разновидности создаются из минералов, газов и даже отходов с целью получения быстрых результатов — иногда в течение нескольких дней.Недостатком синтетических удобрений является их репутация «сжигающих» (т. Е. Убивающих) траву, если они используются слишком жестоко. Они также могут нанести вред окружающей среде и нанести вред здоровью, если они попадут в местный водопровод.
Органические удобрения производятся из живых организмов — от семян хлопка или торфяного мха до гуано летучих мышей, крови или костной муки. Им может потребоваться немного больше времени, чтобы проявить свою магию — часто бывает несколько недель, прежде чем станут видны результаты. Хотя они требуют немного терпения, риски для окружающей среды и здоровья низкие.
Найдите свою формулу.Есть два состава удобрений: жидкие и гранулированные. Жидкие удобрения, которые выпускаются в виде жидкости (требующей разбавления водой) или порошка (к которому следует добавлять воду), как правило, требуют более частого внесения, чем гранулированные. Он также может представлять опасность для окружающей среды, если загрязняет местное водоснабжение в больших количествах, вызывает утечку свинца, кадмия и мышьяка через ливневые стоки и вызывает цветение водорослей, а также создает долгосрочные риски для здоровья населения.Тем не менее, это эффективный способ увидеть быстрые результаты, поэтому он рекомендуется только тогда, когда вам нужны действительно быстрые результаты и вы можете использовать его экономно.
Гранулированные удобрения имеют тенденцию действовать медленно, требуя до месяца или больше для получения результатов, но требуя менее частого последующего наблюдения. Кроме того, в целом он представляет гораздо меньший риск для здоровья, поэтому, как правило, это лучший вариант, если вы не хотите ждать несколько недель, пока ваш двор озеленяется.
Наши лучшие предложения
Фото: amazon.com
Органическое азотное удобрение Milorganite — это продукт на основе гранул с высоким содержанием железа и обычных питательных веществ. Он известен тем, что озеленяет газоны с тех пор, как его впервые начали использовать на полях для гольфа в 1920-х годах. Для его нанесения не требуется вода, и он сохраняется до 10 недель, что делает его незаменимым благодаря мягкому соотношению 5-4-0 NPK.
Он известен тем, что озеленяет газоны с тех пор, как его впервые начали использовать на полях для гольфа в 1920-х годах. Для его нанесения не требуется вода, и он сохраняется до 10 недель, что делает его незаменимым благодаря мягкому соотношению 5-4-0 NPK.
Фото: amazon.com
Это органическое удобрение отличается бережной и надежной системой доставки питательных веществ. Полностью на растительной основе, Ringer Lawn Restore не использует твердые биологические вещества, что избавляет от неприятного запаха, присущего многим органическим удобрениям.Формула 10-0-6 NPK Lawn Restore, покрывающая до 5000 квадратных футов на 25-фунтовый мешок, богата азотом и калием и не содержит фосфатов. Это делает его хорошим выбором для экологичных арендаторов и домовладельцев, которым нужен пышный зеленый газон. Одно приложение длится около 10 недель или дольше.
Фото: amazon.com
Отличный выбор благодаря простоте использования, доступной цене и быстродействующей способности быстро озеленять большую часть травы, Scotts Liquid Turf Builder Lawn Food — лучший выбор среди тех, кто может ‘ Жду результатов.Безопасное для использования на большинстве видов травы, всесезонное удобрение с высоким содержанием азота (с соотношением NPK 29-0-3) и покрывает до 2000 квадратных футов газона на бутылку. Прекрасно подходит в качестве «укола в руку» для неоднородного коричневого газона, который нуждается в быстром омоложении, его эффект может длиться до двух месяцев.
Алгебраическое решение уравнений
Алгебраическое решение уравненийСодержание: Эта страница соответствует § 2.4 (с. 200) текста.
Предлагаемые задачи из текста:
с. 212 # 7, 8, 11, 15, 17, 18, 23, 26, 35, 38, 41, 43, 46, 47, 51, 54, 57, 60, 63, 66, 71, 72, 75, 76, 81, 87, 88, 95, 97
Квадратные уравнения
Уравнения с участием радикалов
Полиномиальные уравнения высшей степени
Уравнения, содержащие дробные выражения или абсолютные значения
Квадратные уравнения
Квадратное уравнение имеет вид ax 2 + bx + c = 0, где a, b и c — числа, а a —
не равно 0.
Факторинг
Этот подход к решению уравнений основан на том факте, что если произведение двух величин равно нулю, то хотя бы одна из величин должна быть равна нулю. Другими словами, если a * b = 0, то либо a = 0, либо b = 0, либо и то, и другое. Для получения дополнительной информации о факторизации многочленов см. Обзорный раздел P.3 (p.26) текста.
Пример 1.
2x 2 — 5x — 12 = 0.
(2x + 3) (x — 4) = 0.
2x + 3 = 0 или x — 4 = 0.
x = -3/2, или x = 4.
Принцип квадратного корня
Если x 2 = k, то x = ± sqrt (k).
Пример 2.
x 2 — 9 = 0.
x 2 = 9.
x = 3 или x = -3.
Пример 3.
Пример 4.
x 2 + 7 = 0.
х 2 = -7.
х = ±.
Обратите внимание, что = =, так что решения
x = ±, два комплексных числа.
Завершение площади
Идея завершения квадрата состоит в том, чтобы переписать уравнение в форме, которая позволяет нам применять квадрат корневой принцип.
Пример 5.
x 2 + 6x — 1 = 0.
x 2 + 6x = 1.
x 2 + 6x + 9 = 1 + 9.
9, прибавленная к обеим сторонам, получена из возведения в квадрат половины коэффициента при x, (6/2) 2 = 9. Причина выбор этого значения заключается в том, что теперь левая часть уравнения представляет собой квадрат бинома (полином с двумя членами). Поэтому эта процедура называется , завершение квадрата .[Заинтересованный читатель может видеть, что это истина, учитывая (x + a) 2 = x 2 + 2ax + a 2 .
Чтобы получить «а» нужно всего лишь разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
(x + 3) 2 = 10.
Теперь мы можем применить принцип квадратного корня и затем решить относительно x.
x = -3 ± sqrt (10).
Пример 6.
2x 2 + 6x — 5 = 0.
2x 2 + 6x = 5.
Метод завершения квадрата, продемонстрированный в предыдущем примере, работает, только если старший коэффициент (коэффициент x 2 ) равен 1. В этом примере старший коэффициент равен 2, но мы можем изменить это, разделив обе части уравнения на 2.
x 2 + 3x = 5/2.
Теперь, когда старший коэффициент равен 1, мы берем коэффициент при x, который теперь равен 3, делим его на 2 и возводим в квадрат, (3/2) 2 = 9/4. Это постоянная, которую мы добавляем к обеим сторонам, чтобы завершить квадрат.
x 2 + 3x + 9/4 = 5/2 + 9/4.
Левая часть — квадрат (x + 3/2). [Проверьте это!]
(х + 3/2) 2 = 19/4.
Теперь мы используем принцип квадратного корня и решаем относительно x.
x + 3/2 = ± sqrt (19/4) = ± sqrt (19) / 2.
x = -3/2 ± sqrt (19) / 2 = (-3 ± sqrt (19)) / 2
До сих пор мы обсуждали три метода решения квадратных уравнений. Что лучше? Это зависит от проблема и ваши личные предпочтения. Уравнение в правильной форме для применения принципа квадратного корня могут быть перегруппированы и решены путем факторинга, как мы видим в следующем примере.
Пример 7.
x 2 = 16.
x 2 — 16 = 0.
(x + 4) (x — 4) = 0.
x = -4 или x = 4.
В некоторых случаях уравнение может быть решено путем факторизации, но факторизация не очевидна.
Метод завершения квадрата всегда будет работать, даже если решения являются комплексными числами, и в этом случае мы извлечем квадратный корень из отрицательного числа.Кроме того, шаги, необходимые для завершения квадрата, следующие: всегда одинаковы, поэтому их можно применить к общему квадратному уравнению
топор 2 + bx + c = 0.
Результатом квадрата этого общего уравнения является формула для решений уравнения называется квадратной формулой.
Квадратичная формула
Решения уравнения ax 2 + bx + c = 0 равны
Мы говорим, что завершение квадрата всегда работает, и мы завершили квадрат в общем случае, где у нас есть a, b и c вместо чисел.Итак, чтобы найти решения для любого квадратного уравнения, запишем его в стандартной форме, чтобы найти значения a, b и c, затем подставьте эти значения в квадратную формулу.
Одним из следствий этого является то, что вам никогда не придется заполнять квадрат, чтобы найти решения квадратного уравнения. Однако процесс завершения квадрата важен по другим причинам, поэтому вам все равно нужно знать, как сделай это!
Примеры использования квадратичной формулы:
Пример 8.
2x 2 + 6x — 5 = 0.
В данном случае a = 2, b = 6, c = -5. Подставляя эти значения в квадратичную формулу, получаем
Обратите внимание, что мы решили это уравнение ранее, заполнив квадрат.
Примечание : Есть два реальных решения. Что касается графиков, есть два пересечения для графика функции f (x) = 2x 2 + 6x — 5.
Пример 9.
4x 2 + 4x + 1 = 0
В этом примере a = 4, b = 4 и c = 1.
В этом примере следует отметить два момента.
- Есть только одно решение. С точки зрения графиков это означает, что существует только один пересечение по оси x.
- Решение упрощено, так что квадратный корень не используется. Это означает, что уравнение могло быть решается факторингом. (Все квадратные уравнения могут быть решены путем разложения на множители ! Я имею в виду, что это могло быть решено легко факторингом.)
4x 2 + 4x + 1 = 0.
(2x + 1) 2 = 0.
х = -1/2.
Пример 10.
х 2 + х + 1 = 0
а = 1, б = 1, с = 1
Примечание: Реальных решений нет. Что касается графиков, то для графика нет перехватов. функции f (x) = x 2 + x + 1. Таким образом, решения сложны, поскольку график y = x 2 + x + 1 не имеет пересечений по x.
Выражение под радикалом в квадратичной формуле, b 2 — 4ac, называется дискриминантом уравнение.Последние три примера иллюстрируют три возможности для квадратных уравнений.
1. Дискриминант> 0. Два реальных решения.
2. Дискриминант = 0. Одно реальное решение.
3. Дискриминант <0. Два сложных решения.
Примечания к проверке решений
Ни один из методов, представленных до сих пор в этом разделе, не может вводить посторонние решения.(См. Пример 3 из раздела Линейные уравнения и моделирование.) Тем не менее, рекомендуется проверить свои решения, потому что при решении уравнений очень легко допустить неосторожные ошибки.
Алгебраический метод, который состоит из обратной подстановки числа в уравнение и проверки того, что полученное утверждение верно, хорошо работает, когда решение «простое», но не очень практично, когда решение предполагает радикальное.
Например, в нашем предпоследнем примере 4x 2 + 4x + 1 = 0 мы нашли одно решение x = -1/2.
Алгебраическая проверка выглядит как
4 (-1/2) 2 +4 (-1/2) + 1 = 0.
4 (1/4) — 2 + 1 = 0.
1-2 + 1 = 0.
0 = 0. Решение проверяет.
В предыдущем примере, 2x 2 + 6x — 5 = 0, мы нашли два реальных решения, x = (-3 ± sqrt (19)) / 2. Конечно, можно проверить это алгебраически, но это не очень просто. В этом случае либо графический проверить или использовать калькулятор для алгебраической проверки быстрее.
Сначала найдите десятичные приближения для двух предложенных решений.
(-3 + sqrt (19)) / 2 = 0,679449.
(-3 — sqrt (19)) / 2 = -3,679449.
Теперь используйте графическую утилиту, чтобы построить график y = 2x 2 + 6x — 5, и проследите график, чтобы приблизительно определить, где х-точки пересечения. Если они близки к указанным выше значениям, вы можете быть уверены, что у вас есть правильные решения. Вы также можете вставить приближенное решение в уравнение, чтобы увидеть, дают ли обе части уравнения примерно те же значения.Однако вам все равно нужно быть осторожным в заявлении о том, что ваше решение является правильным, поскольку оно не точное решение.
Обратите внимание, что если вы начали с уравнения 2x 2 + 6x — 5 = 0 и сразу перешли к графику утилиту для ее решения, то вы не получите точных решений, потому что они иррациональны. Однако, найдя (алгебраически) два числа, которые, по вашему мнению, являются решениями, если графическая утилита показывает, что перехваты очень близко к найденным вами числам, то вы, наверное, правы!
Упражнение 1:
Решите следующие квадратные уравнения.
(а) 3x 2 -5x — 2 = 0. Ответ
(б) (x + 1) 2 = 3. Ответ
(в) x 2 = 3x + 2. Ответ
Вернуться к содержанию
Уравнения с участием радикалов
Уравнения с радикалами часто можно упростить, возведя в соответствующую степень и возведя в квадрат, если радикал является квадратным корнем, кубическим корнем и т. д. Эта операция может вводить посторонние корни, поэтому все решения необходимо проверить.
Если в уравнении только один радикал, то перед возведением в степень вы должны договориться, чтобы радикальный член сам по себе на одной стороне уравнения.
Пример 11.
Теперь, когда мы изолировали радикальный член в правой части, возводим обе части в квадрат и решаем полученное уравнение для x.
Чек:
х = 0
Когда мы подставляем x = 0 в исходное уравнение, мы получаем утверждение 0 = 2, что неверно!
Итак, x = 0 не является решением .
х = 3
Когда мы подставляем x = 3 в исходное уравнение, мы получаем утверждение 3 = 3. Это верно, поэтому x = 3 равно раствор .
Решение : x = 3.
Примечание: Решением является координата x точки пересечения графиков y = x и у = sqrt (х + 1) +1.
Посмотрите, что бы произошло, если бы мы возводили обе части уравнения в квадрат до , выделив радикал срок.
Это хуже того, с чего мы начали!
Если в уравнении более одного радикального члена, то, как правило, мы не можем исключить все радикалы с помощью возведение в степень один раз. Однако мы можем уменьшить количество радикальных членов на , возведя в степень.
Если уравнение включает более одного радикального члена, мы все равно хотим изолировать один радикал с одной стороны и возвести в степень. Затем мы повторяем этот процесс.
Пример 12.
Теперь возведите обе части уравнения в квадрат.
В этом уравнении есть только один радикальный член, поэтому мы добились прогресса! Теперь выделите радикальный член, а затем возведите в квадрат снова обе стороны.
Чек:
Подставляя x = 5/4 в исходное уравнение, получаем
sqrt (9/4) + sqrt (1/4) = 2.
3/2 + 1/2 = 2.
Это утверждение верно, поэтому x = 5/4 является решением.
Примечание по проверке решений:
В этом случае выполнить алгебраическую проверку было несложно. Однако графическая проверка имеет то преимущество, что показывает, что нет никаких решений, которые мы не нашли бы, по крайней мере, в рамках прямоугольника просмотра. Решение — координата x точки пересечения графиков y = 2 и y = sqrt (x + 1) + sqrt (x-1).
Упражнение 2:
Решите уравнение sqrt (x + 2) + 2 = 2x. Ответ
Вернуться к содержанию
Полиномиальные уравнения высшей степени
Мы видели, что любое полиномиальное уравнение второй степени (квадратное уравнение) от одной переменной может быть решено с помощью Квадратичная формула. Полиномиальные уравнения степени больше двух сложнее.Когда мы встречаемся такая проблема, то либо многочлен имеет особую форму, которая позволяет нам разложить его на множители, либо мы должны аппроксимировать решения с графической утилитой.
Нулевая постоянная
Один частый частный случай — отсутствие постоянного члена. В этом случае мы можем исключить одну или несколько полномочий x, чтобы начать задачу.
Пример 13.
Коэффициент2x 3 + 3x 2 -5x = 0.
x (2x 2 + 3x -5) = 0.
Теперь у нас есть произведение x и квадратного многочлена, равного 0, так что у нас есть два более простых уравнения.
x = 0 или 2x 2 + 3x -5 = 0.
Первое уравнение решить несложно. x = 0 — единственное решение. Второе уравнение может быть решено факторингом. Примечание: Если бы мы не смогли разложить квадратичный фактор во втором уравнении, мы могли бы прибегнуть к к использованию квадратичной формулы.[Убедитесь, что вы получили те же результаты, что и ниже.]
x = 0 или (2x + 5) (x — 1) = 0.
Итак, есть три решения: x = 0, x = -5/2, x = 1.
Примечание: Решение находится при пересечении графиков f (x) = 2x 3 + 3x 2 -5x.
по группировке
Пример 14.
x 3 -2x 2 -9x +18 = 0.
Коэффициент при x 2 в 2 раза больше, чем при x 3 , и такое же соотношение существует между коэффициенты при третьем и четвертом членах. Группа термины один и два, а также термины третий и четвертый.
x 2 (x — 2) — 9 (x — 2) = 0.
Эти группы имеют общий множитель (x — 2), поэтому мы можем разложить левую часть уравнения на множители.
(x — 2) (x 2 — 9) = 0.
Всякий раз, когда мы находим продукт, равный нулю, мы получаем два более простых уравнения.
x — 2 = 0 или x 2 — 9 = 0.
x = 2 или (x + 3) (x — 3) = 0.
Итак, есть три решения: x = 2, x = -3, x = 3.
Примечание: Эти решения находятся на пересечении графика f (x) = x 3 -2x 2 -9x +18.
Квадратичная форма
Пример 15.
x 4 — x 2 — 12 = 0.
Этот многочлен неквадратичный, он имеет четвертую степень. Однако его можно рассматривать как квадратичный по x 2 .
(x 2 ) 2 — (x 2 ) — 12 = 0.
Это может помочь вам фактически заменить z на x 2 .
z 2 — z — 12 = 0 Это квадратное уравнение относительно z.
(z — 4) (z + 3) = 0.
z = 4 или z = -3.
Мы еще не закончили, потому что нам нужно найти значения x, которые делают исходное уравнение истинным.Теперь заменим z на x 2 и решите полученные уравнения.
x 2 = 4.
х = 2, х = -2.
х 2 = -3.
x = i , или x = — i.
Итак, есть четыре решения: два реальных и два комплексных.
Примечание: Эти решения находятся из пересечений графика f (x) = x 4 — х 2 — 12.
График f (x) = x 4 — x 2 -12 и масштабирование, показывающее его локальное экстремумы.
Упражнение 3:
Решите уравнение x 4 — 5x 2 + 4 = 0. Ответ
Вернуться к содержанию
Уравнения, содержащие дробные выражения или абсолютные значения
Пример 16.
Наименьший общий знаменатель равен x (x + 2), поэтому мы умножаем обе части на это произведение.
Это уравнение квадратичное. Квадратичная формула дает решения
Проверка необходима, потому что мы умножили обе части на переменное выражение. Используя графическую утилиту, мы убедитесь, что оба этих решения проверяют. Решением является координата x точки пересечения графиков. из y = 1 и y = 2 / x-1 / (x + 2).
Пример 17.
5 | х — 1 | = х + 11.
Ключ к решению уравнения с абсолютными значениями — помнить, что величина внутри абсолютного значения столбцы могут быть положительными или отрицательными. У нас будет два отдельных уравнения, представляющих разные возможности, и все решения должны быть проверены.
Дело 1 . Предположим, что x — 1> = 0.Тогда | х — 1 | = x — 1, поэтому мы имеем уравнение
5 (x — 1) = x + 11.
5x — 5 = x + 11.
4x = 16.
x = 4, и это решение проверяет, потому что 5 * 3 = 4 + 11.
Случай 2. Предположим, что x — 1 <0. Тогда x - 1 отрицательно, поэтому | х - 1 | = - (х - 1). Этот точка часто сбивает студентов с толку, потому что это выглядит так, как будто мы говорим, что абсолютное значение выражения отрицательно, но это не так.Выражение (x - 1) уже отрицательное, поэтому - (x - 1) положительное.
Теперь наше уравнение принимает вид
.-5 (x — 1) = x + 11.
-5x + 5 = x + 11.
-6x = 6.
x = -1, и это решение проверяет, потому что 5 * 2 = -1 + 11.
Если вы используете Java Grapher для графической проверки, обратите внимание, что abs () является абсолютным значением, поэтому вы должны построить график
5 * abs (x — 1) — x — 11 и посмотрите на пересечения по x, или вы можете найти решение как x-координаты точки пересечения графиков y = x + 11 и y = 5 * abs (x-1).
Упражнение 4:
(а) Решите уравнение Ответ
(b) Решите уравнение | х — 2 | = 2 — x / 3 Ответ
Вернуться к содержанию
Борьба с травянистыми сорняками до появления всходов | Спринг-Вэлли
Dimension®
РАЗМЕР (дитиопир) обеспечивает посезонную предвсходовую борьбу с самыми жесткими травами, а также подавляет больше однолетних широколистных сорняков с мелкими семенами, чем любой другой гербицид. РАЗМЕР можно использовать в качестве предвсходового средства перед прорастанием злаковых трав или в качестве послевсходового внесения при кущении до 3-х листьев. Когда дело доходит до предотвращения сорняков на полях для гольфа, DIMENSION предлагает широкий спектр вариантов применения (весной, летом и осенью) и борется с мятликом однолетним, а также с 25 другими жесткими травами и широколистными сорняками. Для достижения наилучших результатов нанесите РАЗМЕР с минимальной скоростью 0,125–0,50 фунта A.I. в северном климате (обеспечивает примерно 90-180-дневный контроль), и.25-0,50 фунтов. А.И. на акр в южном климате (для контроля на 120–180 дней), но не более 1,5 фунта. А.И. за акр в год. Компоненты в РАЗМЕР не эффективны, если они не активированы минимальным количеством осадков 0,5 дюйма или верхним орошением.
| Размерные смеси | Номер позиции | Состав | Этикетка | SDS |
| 18-0-3 + .10 Размер | 2019127 | 25% XCU | Этикетка | SDS |
| 19-0-0 +.10 Размер | 2025326 | 100% восстановление | Этикетка | SDS |
| 13-0-0 + .125 Размер | 2014746 | 100% восстановление | Этикетка | SDS |
| 19-0-3 + .125 Размер | 2015530 | 30% XCU, СС | Этикетка | SDS |
| 13-0-0 + .15 Размер | 2014743 | 100% восстановление | Этикетка | SDS |
| 18-0-3 +.15 Размер | 2019123 | 25% XCU, MOP | Этикетка | SDS |
| 19-0-3 + .15 Размер | 2015532 | 30% XCU, СС | Этикетка | SDS |
| 13-0-5 + .17 Размер | 2014677 | 30% UFLEXX, MOP | Этикетка | SDS |
| 19-0-5 + .25 Размер | 2078585 | 25% ULFEXX, 20% Top Cut, MOP | Этикетка | SDS |
Продиамин
Продиамин — это экономичный гербицид до появления всходов, который обеспечивает низкую дозу внесения и очень эффективен против более 30 травянистых и широколистных сорняков, включая крабовую траву, гусиный трава и мятлик однолетний.Продиамин не оставляет пятен и предлагает широкий спектр возможностей применения. Однократное внесение — это все, что нужно для борьбы в течение всего сезона, поскольку многие специалисты по газону предпочитают применять Продиамин осенью после того, как температура почвы опустится ниже 50 ° F. Продиамин имеет самую низкую растворимость и летучесть в воде и остается в пределах полдюйма верхнего слоя почвы. Для достижения наилучших результатов применяйте продиамин с минимальной скоростью 0,5 фунта. А.И. на акр для контроля до 12 недель, 1,00 фунт. А.И. на акр на срок до 20 недель и 1.50 фунтов. А.И. на акр до 32-недельного контроля.
Компоненты продиамина не эффективны, если они не активированы минимальным количеством осадков 0,5 дюйма или верхним орошением.
| Смеси продиамина | Номер позиции | Состав | Этикетка | SDS |
| 5-0-10 + .20 Продиамин | 2070427 | Все минералы, MOP | Этикетка | SDS |
| 19-0-3 + .20 Продиамин | 2015542 | 25% XCU, MOP | Этикетка | SDS |
| 12-0-0 +.29 Продиамин | 2010234 | 100% восстановление | Этикетка | SDS |
| 15-0-3 + .29 Продиамин | 2016221 | 25% XCU, MOP | Этикетка | SDS |
| 17-0-0 + .29 Продиамин | 2019881 | 100% восстановление | Этикетка | SDS |
| 17-0-0 + 0,37 Продиамин | 2019871 | 100% восстановление | Этикетка | SDS |
| 13-0-5 +.42 Продиамин | 2014731 | 100% восстановление, MOP | Этикетка | SDS |
| 18-0-3 + .42 Продиамин | 2019115 | 25% XCU, MOP | Этикетка | SDS |
| 19-0-2 + .42 Продиамин | 2015527 | 25% UFLEXX, MOP | Этикетка | SDS |
| 19-0-3 + .42 Продиамин | 2015547 | 100% восстановление, MOP | Этикетка | SDS |
| 13-0-5 +.58 Продиамин | 2014679 | 100% восстановление, MOP | Этикетка | SDS |
Оксадиазон
Оксадиазон — это премиальный продукт для борьбы с сорняками до появления всходов, предназначенный для использования на разновидностях мятлика многолетнего, бентграсса, травы бермудских островов, травы буйвола, райграсс многолетнего, травы святого Августина, морского паспала, овсяницы высокорослой и зойсиаграсса. Также для использования вокруг декоративных кустарников, виноградных лоз, деревьев и почвенных покровов. Oxadiazon, доступный в двух вариантах, будет контролировать Crabgrass, Goosegrass, Poa annua, однолетнюю осоку и другие перечисленные сорняки на полях для гольфа, в парках, а также на развлекательных и декоративных газонах.
| Смеси оксадиазона | Номер позиции | Состав | Этикетка | SDS |
| 5-0-20 + .10 Оксадиазон | 2070413 | Все минералы, MOP | Этикетка | SDS |
| 5-0-20 + .15 Оксадиазон | 2070414 | Все минералы, MOP | Этикетка | SDS |
Прямоугольная система координат
Точка, которая делит пополам отрезок прямой, образованный двумя точками (x1, y1) и (x2, y2), называется средней точкой. Имеются две точки (x1, y1) и (x2, y2). ), середина — это упорядоченная пара, заданная формулой (x1 + x22, y1 + y22).и задается следующей формулой:
Средняя точка — это упорядоченная пара, образованная путем нахождения среднего значения x и среднего значения y данных точек.
Пример 8: Вычислите среднюю точку между (−1, −2) и (7, 4).
Решение: Сначала вычислите среднее значение x — и y — значений заданных точек.
Затем сформируйте среднюю точку в виде упорядоченной пары, используя усредненные координаты.
Чтобы убедиться, что это действительно средняя точка, вычислите расстояние между двумя заданными точками и убедитесь, что результат равен сумме двух равных расстояний от конечных точек до этой средней точки. Эта проверка предоставляется читателю в качестве упражнения.
Попробуй! Найдите середину между (−6, 5) и (6, −11).
Тематические упражнения
Часть A: Заказанные пары
Укажите координаты точек A , B , C , D и E .
1.
2.
3.
4.
5.
6.
Изобразите данный набор упорядоченных пар.
7. {(−4, 5), (−1, 1), (−3, −2), (5, −1)}
8. {(−15, −10), (−5, 10), (15, 10), (5, −10)}
9. {(−2, 5), (10, 0), (2, −5), (6, −10)}
10. {(−8, 3), (−4, 6), (0, −6), (6, 9)}
11. {(−10, 5), (20, −10), (30, 15), (50, 0)}
12. {(−53, −12), (- 13, 12), (23, −1), (53, 1)}
13. {(-35, -43), (25, 43), (1, -23), (0, 1)}
14.{(−3,5, 0), (−1,5, 2), (0, 1,5), (2,5, −1,5)}
15. {(-0,8, 0,2), (-0,2, -0,4), (0, -1), (0,6, -0,4)}
16. {(-1,2, -1,2), (-0,3, -0,3), (0, 0), (0,6, 0,6), (1,2, 1,2)}
Укажите квадрант, в котором находится данная точка.
17. (−3, 2)
18. (5, 7)
19. (−12, −15)
20. (7, −8)
21. (-3,8, 4.6)
22. (17,3, 1,9)
23. (−18, −58)
24. (34, −14)
25. x> 0 и y <0
26. x <0 и y <0
27. x <0 и y> 0
28. x> 0 и y> 0
Средняя цена галлона обычного неэтилированного бензина в городах США представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.
Источник: Бюро статистики труда.
29. Какова была средняя цена галлона неэтилированного бензина в 2004 году?
30. Какова была средняя цена галлона неэтилированного бензина в 1976 году?
31. В какие годы средняя цена галлона неэтилированного бензина составляла 1,20 доллара США?
32. Насколько выросла цена галлона бензина с 1980 по 2008 год?
33.На сколько процентов увеличилась цена галлона неэтилированного бензина с 1976 по 1980 год?
34. Каков процент увеличения цены галлона неэтилированного бензина с 2000 по 2008 год?
Средняя цена на универсальную белую муку в городах США с 1980 по 2008 год представлена на следующем линейном графике. Используйте график, чтобы ответить на следующие вопросы.
Источник: Бюро статистики труда.
35. Какова была средняя цена за фунт универсальной белой муки в 2000 году?
36. Какова была средняя цена за фунт универсальной белой муки в 2008 году?
37. В каком году мука стоила в среднем 0,25 доллара за фунт?
38. В какие годы цена на муку составляла в среднем 0,20 доллара за фунт?
39. Каков процент увеличения производства муки с 2000 по 2008 год?
40.Каков процент увеличения муки с 1992 по 2000 год?
С учетом следующих данных создайте линейный график.
41. Процент от общего числа выпускников средней школы, поступивших в колледж.
| Год | Процент |
|---|---|
| 1969 | 36% |
| 1979 | 40% |
| 1989 | 47% |
| 1999 | 42% |
Источник: Сборник статистики образования.
42. Средняя дневная температура в мае в градусах Фаренгейта.
| Экзамен | Температура |
|---|---|
| 8:00 | 60 |
| 12:00 | 72 |
| 16:00 | 75 |
| 20:00 | 67 |
| 12:00 | 60 |
| 4:00 | 55 |
Вычислите площадь формы, образованной соединением следующего набора вершин.
43. {(0, 0), (0, 3), (5, 0), (5, 3)}
44. {(−1, −1), (−1, 1), (1, −1), (1, 1)}
45. {(−2, −1), (−2, 3), (5, 3), (5, −1)}
46. {(−5, −4), (−5, 5), (3, 5), (3, −4)}
47. {(0, 0), (4, 0), (2, 2)}
48. {(−2, −2), (2, −2), (0, 2)}
49. {(0, 0), (0, 6), (3, 4)}
50. {(−2, 0), (5, 0), (3, −3)}
Часть B: Формула расстояния
Рассчитайте расстояние между заданными двумя точками.
51. (−5, 3) и (−1, 6)
52. (6, −2) и (−2, 4)
53. (0, 0) и (5, 12)
54. (−6, −8) и (0, 0)
55. (−7, 8) и (5, −1)
56. (-1, -2) и (9, 22)
57. (−1, 2) и (−7/2, −4)
58. (−12, 13) и (52, −113)
59. (−13, 23) и (1, −13)
60. (12, −34) и (32, 14)
61.(1, 2) и (4, 3)
62. (2, −4) и (−3, −2)
63. (-1, 5) и (1, -3)
64. (1, −7) и (5, −1)
65. (−7, −3) и (−1, 6)
66. (0, 1) и (1, 0)
67. (-0,2, -0,2) и (1,8, 1,8)
68. (1,2, −3,3) и (2,2, −1,7)
Для каждой задачи покажите, что три точки образуют прямоугольный треугольник.
69.(−3, −2), (0, −2) и (0, 4)
70. (7, 12), (7, −13) и (−5, −4)
71. (-1,4, 0,2), (1, 2) и (1, -3)
72. (2, -1), (-1, 2) и (6, 3)
73. (−5, 2), (−1, −2) и (−2, 5)
74. (1, −2), (2, 3) и (−3, 4)
Равнобедренные треугольники имеют две ноги равной длины. Для каждой задачи покажите, что следующие точки образуют равнобедренный треугольник.
75.(1, 6), (−1, 1) и (3, 1)
76. (−6, −2), (−3, −5) и (−9, −5)
77. (−3, 0), (0, 3) и (3, 0)
78. (0, -1), (0, 1) и (1, 0)
Вычислите площадь и периметр треугольников, образованных следующим набором вершин.
79. {(−4, −5), (−4, 3), (2, 3)}
80. {(−1, 1), (3, 1), (3, −2)}
81. {(−3, 1), (−3, 5), (1, 5)}
82.{(−3, −1), (−3, 7), (1, −1)}
Часть C: Формула средней точки
Найдите середину между заданными двумя точками.
83. (−1, 6) и (−7, −2)
84. (8, 0) и (4, −3)
85. (−10, 0) и (10, 0)
86. (−3, −6) и (−3, 6)
87. (−10, 5) и (14, −5)
88. (0, 1) и (2, 2)
89. (5, −3) и (4, −5)
90.(0, 0) и (1, 1)
91. (-1, -1) и (4, 4)
92. (3, −5) и (3, 5)
93. (−12, −13) и (32, 73)
94. (34, −23) и (18, −12)
95. (53, 14) и (−16, −32)
96. (−15, −52) и (710, −14)
97. Дан прямоугольный треугольник, образованный вершинами (0, 0), (6, 0) и (6, 8), покажите, что середины сторон образуют прямоугольный треугольник.
98. Для равнобедренного треугольника, образованного вершинами (−10, −12), (0, 12) и (10, −12), покажите, что середины сторон также образуют равнобедренный треугольник.
99. Вычислите площадь треугольника, образованного вершинами (−4, −3), (−1, 1) и (2, −3). (Подсказка: вершины образуют равнобедренный треугольник.)
100. Вычислите площадь треугольника, образованного вершинами (−2, 1), (4, 1) и (1, −5).
Часть D. Темы дискуссионной доски
101.Изучите и обсудите жизнь и вклад в математику Рене Декарта.
102. Изучите и обсудите историю прямоугольного треугольника и теоремы Пифагора.
103. Что такое тройка Пифагора? Приведите несколько примеров.
104. Объясните, почему нельзя использовать линейку для вычисления расстояния на графике.
105. Как разделить отрезок пополам с помощью циркуля и линейки?
Квадратичная формула: решения и дискриминант
Purplemath
Приведем еще несколько примеров.
Решите
x ( x — 2) = 4. Округлите ответ до двух десятичных знаков.
Я не только не могу применить квадратичную формулу на данном этапе, но и не могу использовать множители. Почему? Потому что это уравнение пока что в правильном виде.
И я, , конечно, не могу с невозмутимым видом утверждать, что « x = 4, x — 2 = 4», потому что это , а не , как работает «решение с использованием факторинга».
Независимо от того, какой метод решения я собираюсь использовать — факторизую ли я на множители или использую квадратичную формулу для поиска ответов — я должен сначала преобразовать уравнение в форму «(квадратичный) = 0».
MathHelp.com
Первое, что я сделаю здесь, это умножу на левую часть, а затем переместу 4 из правой части в левую:
x ( x -2) = 4
x 2 — 2 x = 4
x 2 — 2 x — 4 = 0
Поскольку нет множителей при (1) (- 4) = –4, которые в сумме дают –2, то эта квадратичная величина не множится.(Другими словами, невозможно, чтобы решение « x = 4, x — 2 = 4» с ложным факторингом могло быть хоть немного правильным.)
Значит, факторинг не сработает, но я могу использовать квадратичную формулу; в этом случае я вставлю значения a = 1, b = –2 и c = –4:
.Тогда ответ:
x = –1.24, x = 3,24 с округлением до двух десятичных знаков.
Для справки, вот как выглядит график соответствующей квадратичной, y = x 2 -2 x -4, выглядит так:
Как видите, решения квадратичной формулы совпадают с интерцепциями x . Точки пересечения графика с осью x дают значения, которые решают исходное уравнение.
Существует еще одна связь между решениями из квадратичной формулы и графиком параболы: вы можете определить, сколько интервалов x вы получите, исходя из значения внутри квадратного корня. Аргумент (то есть содержание) квадратного корня, являющийся выражением b 2 — 4 ac , называется «дискриминантом», потому что, используя его значение, вы можете «различать» (что уметь различать) различные типы решений.
В данном случае значение дискриминанта b 2 — 4 ac было 20; в частности, значение было , а не ноль, и было , а не отрицательным. Поскольку значение не было отрицательным, уравнение должно было иметь по крайней мере одно (действительное) решение; поскольку значение не было нулевым, два решения должны были быть разными (то есть они должны были отличаться друг от друга).
Решить 9
x 2 + 12 x + 4 = 0.Оставьте свой ответ в точной форме.
Используя a = 9, b = 12 и c = 4, квадратичная формула дает мне:
Тогда ответ:
В первом примере на этой странице я получил два решения, потому что значение дискриминанта (то есть значение внутри квадратного корня) было ненулевым и положительным.В результате часть формулы «плюс-минус» дала мне два различных значения; один для «плюсовой» части числителя и другой для «минусовой» части. Однако в этом случае квадратный корень уменьшился до нуля, поэтому плюс-минус ни для чего не учитывался.
Такое решение, при котором вы получаете только одно значение, потому что «плюс или минус ноль» ничего не меняет, называется «повторяющимся» корнем, потому что x равно
–2 / 3 , но оно равно этому значению как бы вдвое: –2 / 3 + 0 и –2 / 3 — 0.Вы можете лучше увидеть это повторение, если разложите квадратичный множитель (и, поскольку решения были хорошими точными дробями, квадратичный должен множить ): 9 x 2 + 12 x + 4 = (3 x + 2) (3 x + 2) = 0, поэтому первый множитель дает нам 3 x + 2 = 0, поэтому
x = –2 / 3 , и (из второго, идентичный коэффициент) 3 x + 2 = 0, поэтому x = –2 / 3 снова.Каждый раз, когда вы получаете ноль внутри квадратного корня квадратной формулы, вы получаете только одно решение уравнения в смысле получения одного числа, которое решает уравнение. Но вы получите два решения в том смысле, что одно значение будет подсчитано дважды. Другими словами, дискриминант (то есть выражение b 2 — 4 ac ) с нулевым значением означает, что вы получите одно «повторяющееся» значение решения.
Ниже показан график связанной функции, y = 9 x 2 + 12 x + 4, выглядит так:
Парабола только касается оси x при
x = –2 / 3 ; это на самом деле не пересекает.Это соотношение всегда верно: если у вас есть корень, который встречается ровно дважды (или, что одно и то же, если вы получаете ноль внутри квадратного корня), то график будет «целовать» ось в значении решения, но он не пройдет через ось.Поскольку нет множителей при (3) (2) = 6, которые в сумме дают 4, эта квадратичная величина не множится. Но квадратичная формула всегда работает; в этом случае я вставлю значения a = 3, b = 4 и c = 2:
На данный момент у меня есть отрицательное число внутри квадратного корня.Если вы еще не узнали о комплексных числах, вам придется остановиться на этом, и ответ будет «нет решения»; если вы знаете комплексные числа, то можете продолжить вычисления:
Таким образом, в зависимости от вашего уровня обучения ваш ответ будет одним из следующих:
решения в виде вещественных чисел: нет решения
комплексно-числовых решений:
Партнер
Но знаете ли вы о комплексах или нет, вы знаете, что вы не можете изобразить свой ответ, потому что вы не можете изобразить квадратный корень из отрицательного числа на правильном декартовом месте.На оси x таких значений нет. Поскольку вы не можете найти графическое решение квадратичной функции, разумно не должно быть никаких перехватов x (потому что вы можете построить график с перехватом x ).
Вот график связанной функции, y = 3 x 2 + 4 x + 2:
Как видите, график не пересекает ось x и даже не касается ее.Это соотношение всегда верно: если вы получите отрицательное значение внутри квадратного корня, тогда не будет решения действительного числа и, следовательно, не будет x -перехватов. Другими словами, если дискриминант (являющийся выражением b 2 — 4 ac ) имеет отрицательное значение, то у вас не будет графических нулей.
(взаимосвязь между дискриминантом (являющимся значением внутри квадратного корня), типом решений (два различных решения, одно повторяющееся решение или отсутствие графических решений) и количеством x -перехватываний на графике (два , один или ни один) сведены в диаграмму на следующей странице.)
URL: https://www.purplemath.com/modules/quadform2.htm
Решите квадратное уравнение с помощью программы «Пошаговое решение математических задач»
Решение уравнений — центральная тема алгебры. Все приобретенные навыки в конечном итоге приводят к способности решать уравнения и упрощать решения.В предыдущих главах мы решали уравнения первой степени. Теперь у вас есть необходимые навыки для решения уравнений второй степени, которые известны как квадратных уравнений .
КВАДРАТИКА, РЕШЕННАЯ ФАКТОРИНГОМ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите квадратное уравнение.
- Приведите квадратное уравнение в стандартную форму.
- Решите квадратное уравнение, вычислив множители.
Квадратное уравнение — это полиномиальное уравнение, которое содержит вторую степень, но не более высокую степень переменной.
Стандартная форма квадратного уравнения — ax 2 + bx + c = 0, когда a ≠ 0 и a, b и c — действительные числа.
Все квадратные уравнения могут быть представлены в стандартной форме, и любое уравнение, которое может быть преобразовано в стандартную форму, является квадратным уравнением. Другими словами, стандартная форма представляет все квадратные уравнения.
Решение уравнения иногда называют корнем уравнения .
| Эта теорема доказана в большинстве учебных пособий по алгебре. |
Важная теорема, которую невозможно доказать на уровне этого текста, гласит: «Каждое полиномиальное уравнение степени n имеет ровно n корней». Использование этого факта говорит нам, что квадратные уравнения всегда будут иметь два решения. Возможно, что два решения равны.
| Квадратное уравнение будет иметь два решения, поскольку оно имеет степень два. |
Самый простой метод решения квадратичных вычислений — факторинг.Этот метод не всегда можно использовать, потому что не все многочлены факторизуемы, но он используется всякий раз, когда факторизация возможна.
Метод решения с помощью факторизации основан на простой теореме.
Если AB = 0, то либо A = 0, либо B = 0.
| Другими словами, если произведение двух факторов равно нулю, то по крайней мере один из факторов равен нулю. |
Мы не будем пытаться доказывать эту теорему, но внимательно отметим, что в ней говорится. Мы никогда не сможем перемножить два числа и получить ответ ноль, если хотя бы одно из чисел не равно нулю.Конечно, оба числа могут быть нулевыми, поскольку (0) (0) = 0.
Решение Шаг 1 Приведите уравнение в стандартную форму.
| Мы должны вычесть 6 с обеих сторон. |
Шаг 2 Полностью разложить на множители.
| Вспомните, как разложить на множители трехчлены. |
Шаг 3 Установите каждый коэффициент равным нулю и решите относительно x. Поскольку у нас есть (x — 6) (x + 1) = 0, мы знаем, что x — 6 = 0 или x + 1 = 0, и в этом случае x = 6 или x = — 1.
| Здесь применяется приведенная выше теорема, согласно которой хотя бы один из факторов должен иметь нулевое значение. |
Шаг 4 Проверьте решение в исходном уравнении. Если x = 6, то x 2 — 5x = 6 становится
| Проверка ваших решений — верный способ узнать, правильно ли вы решили уравнение. |
Следовательно, x = 6 является решением. Если x = — 1, то x 2 — 5x = 6 становится
Следовательно, — 1 — решение.
Решения могут быть указаны либо записью x = 6 и x = — 1, либо использованием обозначения набора и записи {6, — 1}, что мы читаем «набор решений для x равен 6 и — 1». В этом тексте мы будем использовать обозначения набора.
| В этом примере 6 и -1 называются элементами набора. |
| Обратите внимание, что в этом примере уравнение уже имеет стандартную форму. |
| Опять же, проверка решений убедит вас, что вы не допустили ошибки при решении уравнения. также называют корнями уравнения. |
| (x + 1) — наименьший общий знаменатель всех дробей в уравнении. Помните, что каждый член уравнения нужно умножить на (x + 1). |
Проверьте решения в исходном уравнении.
| Проверьте исходное уравнение, чтобы убедиться, что знаменатель не равен нулю. |
| Обратите внимание, что здесь два решения равны.Это происходит только тогда, когда трехчлен является полным квадратом. |
НЕПОЛНАЯ КВАДРАТИКА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите неполное квадратное уравнение.
- Решите неполное квадратное уравнение.
Если уравнение представлено в стандартной форме ax 2 + bx + c = 0, либо b = 0, либо c = 0, уравнение представляет собой неполное квадратичное уравнение .
Пример 1
5x 2 -10 = 0 является неполным квадратичным, так как средний член отсутствует и, следовательно, b = 0.
Когда вы сталкиваетесь с неполной квадратичной с c — 0 (отсутствует третий член), ее все же можно решить с помощью факторизации.
| x — общий множитель. Произведение двух факторов равно нулю. Поэтому мы используем теорему из предыдущего раздела. Проверьте эти решения. |
Обратите внимание, что если член c отсутствует, вы всегда можете множить x из других членов. Это означает, что во всех таких уравнениях нуль будет одним из решений.
Неполная квадратичная с отсутствующим членом b должна быть решена другим методом, поскольку факторизация будет возможна только в особых случаях.
Пример 3 Решите относительно x, если x 2 — 12 = 0.
Решение Поскольку x 2 -12 не имеет общего множителя и не является разностью квадратов, его нельзя разложить на рациональные множители. Но из предыдущих наблюдений мы имеем следующую теорему.
| Обратите внимание, что есть два значения, которые в квадрате будут равны A. |
Используя эту теорему, имеем
| Проверьте эти решения. |
| Добавьте 10 с каждой стороны. Проверьте эти решения. |
| Здесь 7x — общий множитель. Проверьте эти решения. |
Обратите внимание, что в этом примере у нас есть квадрат числа, равного отрицательному числу. Это никогда не может быть правдой в действительной системе счисления, и поэтому у нас нет реального решения.
ЗАВЕРШЕНИЕ ПЛОЩАДИ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите трехчлен полного квадрата.
- Завершите третий член, чтобы получить трехчлен в виде полного квадрата.
- Решите квадратное уравнение, заполнив квадрат.
Из вашего опыта факторинга вы уже понимаете, что не все многочлены факторизуемы. Следовательно, нам нужен метод решения квадратичных вычислений, которые не подлежат факторизации.Необходимый метод называется «завершение квадрата».
Сначала давайте рассмотрим значение «трехчлена полного квадрата». Когда мы возводим двучлен в квадрат, мы получаем полный квадрат трехчлена. Общая форма: (a + b) 2 = a 2 + 2ab + b 2 .
| Помните, возведение бинома в квадрат означает его умножение на само себя. |
Из общей формы и этих примеров мы можем сделать следующие наблюдения относительно трехчлена полного квадрата.
- Два из трех членов — полные квадраты. 4x 2 и 9 в первом примере, 25x 2 и 16 во втором примере, а также 2 и b 2 в общем виде.
Другими словами, первое и третье члены являются точными квадратами. - Другой член — это произведение квадратных корней из двух других членов, умноженное на два плюс или минус.
Член -7 сразу говорит, что это не может быть трехчлен полного квадрата.Задача при заполнении квадрата состоит в том, чтобы найти число, которое заменит -7 таким образом, чтобы получился идеальный квадрат.
Рассмотрим эту задачу: заполните пробел так, чтобы «x 2 + 6x + _______» было трехчленом в виде полного квадрата. Из двух условий для трехчлена полного квадрата мы знаем, что пробел должен содержать полный квадрат и что 6x должно быть удвоенным произведением квадратного корня x 2 и числа в пробеле. Поскольку x уже присутствует в 6x и является квадратным корнем из x 2 , то 6 должно быть в два раза больше квадратного корня из числа, которое мы помещаем в пробел.Другими словами, если мы сначала возьмем половину 6, а затем возведем в квадрат этот результат, мы получим необходимое число для бланка.
Следовательно, x 2 + 6x + 9 — это трехчлен полного квадрата.
Теперь давайте рассмотрим, как мы можем использовать завершение квадрата для решения квадратных уравнений.
Пример 5 Решите x 2 + 6x — 7 = 0, заполнив квадрат.
| Напомним, что вместо -7, +9 сделает выражение идеальным квадратом. |
Решение Сначала мы замечаем, что член -7 необходимо заменить, если мы хотим получить трехчлен в виде полного квадрата, поэтому мы перепишем уравнение, оставив пустое поле для нужного числа.
Здесь будьте осторожны, чтобы не нарушить никаких правил алгебры. Например, обратите внимание, что вторая форма появилась в результате добавления +7 к обеим сторонам уравнения. Никогда не добавляйте что-либо к одной стороне, не добавляя то же самое к другой стороне.
Теперь мы находим половину 6 = 3 и 3 2 = 9, чтобы получить число для пробела.Опять же, если мы поместим 9 в пустое поле, мы также должны добавить 9 к правой стороне.
| Помните, что если 9 добавляется в левую часть уравнения, ее также необходимо добавлять в правую часть. |
Теперь разложите на множители трехчлена полного квадрата, что дает
| Теперь x 2 + 6x + 9 можно записать как (x + 3) 2 . |
| Таким образом, 1 и -7 являются решениями или корнями уравнения. |
Пример 6 Решите 2x 2 + 12x — 4 = 0, заполнив квадрат.
Решение Эта проблема порождает еще одну трудность. Первый член, 2x 2 , не является полным квадратом.
Мы исправим это, разделив все члены уравнения на 2 и получим
| Другими словами, получите коэффициент 1 для члена x 2 . |
Теперь прибавим 2 к обеим сторонам, получив
| Опять же, это более лаконично. |
Пример 7 Решите 3x 2 + 7x — 9 = 0, заполнив квадрат.
Решение Шаг 1 Разделите все члены на 3.
| Опять же, получим коэффициент 1 для x 2 , разделив на 3. |
Шаг 2 Перепишите уравнение, оставив пробел для члена, необходимого для завершения квадрата.
Шаг 3 Найдите квадрат половины коэффициента при x и прибавьте к обеим сторонам.
| Это выглядит сложным, но мы следуем тем же правилам, что и раньше. |
Шаг 4 Разложите квадрат на множители.
Факторинг никогда не должен быть проблемой, поскольку мы знаем, что у нас есть полный квадратный трехчлен, что означает, что мы находим квадратные корни из первого и третьего членов и используем знак среднего члена.
Если у вас возникнут какие-либо затруднения, вам следует еще раз повторить арифметику при сложении чисел справа.
Теперь у нас
Шаг 5 Извлеките квадратный корень из каждой части уравнения.
Шаг 6 Решите относительно x (два значения).
| не может быть упрощено. Мы могли бы также записать решение этой проблемы в более сжатой форме как |
Выполните шаги, описанные в предыдущем вычислении, а затем обратите особое внимание на последнее значение. Каков вывод, когда квадрат количества равен отрицательному числу? «Реального решения нет.«
| Какое действительное число мы можем возвести в квадрат и получить -7? |
Таким образом, чтобы решить квадратное уравнение, заполнив квадрат, следуйте этому пошаговому методу.
Шаг 1 Если коэффициент при x2 не равен 1, разделите все члены на этот коэффициент.
Шаг 2 Перепишите уравнение в виде x2 + bx + _______ = c + _______.
Шаг 3 Найдите квадрат половины коэффициента члена x и добавьте эту величину к обеим сторонам уравнения.
Шаг 4 Разложите заполненный квадрат на множители и сложите числа в правой части уравнения.
Шаг 5 Найдите квадратный корень из каждой части уравнения.
Шаг 6 Решите относительно x и упростите.
Если шаг 5 невозможен, уравнение не имеет реального решения.
| Эти шаги помогут в решении уравнений в следующем упражнении. |
КВАДРАТИЧЕСКАЯ ФОРМУЛА
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Решите общее квадратное уравнение, заполнив квадрат.
- Решите любое квадратное уравнение, используя формулу корней квадратного уравнения.
- Решите квадратное уравнение, заполнив квадрат.
Стандартная форма квадратного уравнения — ax 2 + bx + c = 0. Это означает, что каждое квадратное уравнение может быть представлено в этой форме. В некотором смысле, тогда ax 2 + bx + c = 0 представляет все квадраты. Если вы сможете решить это уравнение, у вас будет решение всех квадратных уравнений.
Решим общее квадратное уравнение методом завершения квадрата.
| Это необходимо для получения члена x 2 с коэффициентом 1. Это мы проделывали в предыдущем разделе много раз. |
| Надо прибавить с каждой стороны. |
Эта форма называется квадратной формулой и представляет собой решение всех квадратных уравнений.
| Запомните это выражение. |
Чтобы использовать формулу квадратного уравнения, вы должны указать a, b и c.Для этого данное уравнение всегда необходимо оформлять в стандартном виде.
| Осторожно подставьте значения a, b и c в формулу. |
Не каждое квадратное уравнение имеет реальное решение.
| Это уравнение уже имеет стандартную форму. |
Реального решения нет, так как -47 не имеет действительного квадратного корня.
| Опять же, это уравнение в стандартной форме. |
Теперь это решение следует упростить.
ПРОБЛЕМЫ СО СЛОВОМ
ЗАДАЧИ
По завершении этого раздела вы сможете:
- Определите текстовые задачи, для решения которых требуется квадратное уравнение.
- Решать текстовые задачи, связанные с квадратными уравнениями.
Некоторые типы словесных задач могут быть решены с помощью квадратных уравнений. Процесс определения и постановки проблемы такой же, как и в главе 5, но с проблемами, решаемыми квадратичными методами, вы должны быть очень осторожны, проверяя решения в самой проблеме.Физические ограничения внутри проблемы могут устранить одно или оба решения.
Пример 1 Если длина прямоугольника на 1 единицу больше, чем в два раза ширины, а его площадь составляет 55 квадратных единиц, найдите длину и ширину.
Решение Формула площади прямоугольника: Площадь = Длина X Ширина. Пусть x = ширина, 2x + 1 = длина.
| Если x представляет ширину, то 2x представляет удвоенную ширину, а 2x + 1 представляет единицу более чем удвоенную ширину. |
| Приведите квадратное уравнение в стандартную форму. Эта квадратичная величина может быть решена путем факторизации. |
На этом этапе вы можете видеть, что решение x = -11/2 недействительно, поскольку x представляет собой измерение ширины, а отрицательные числа не используются для таких измерений. Следовательно, решение
ширина = x = 5, длина = 2x + 1 = 11.
| Измерение не может быть отрицательным значением. |
| Значение x, обратное. Помните, что ЖК-дисплей означает наименьший общий знаменатель. Каждый член нужно умножить в 10 раз. Опять же, эту квадратичную величину можно разложить на множители. |
Оба решения проверяют. Следовательно, набор решений есть.
| Есть два решения этой проблемы. |
Пример 3 Если определенное целое число вычитается из его квадрата, умноженного на 6, получается 15.Найдите целое число.
Решение Пусть x = целое число. Тогда
Поскольку ни одно из решений не является целым числом, проблема не имеет решения.
| У вас может возникнуть соблазн указать эти значения в качестве решения, если вы не обратили пристальное внимание на тот факт, что проблема запрашивала целое число. |
Пример 4 Управляющий фермой имеет под рукой 200 метров забора и желает оградить прямоугольное поле так, чтобы его площадь составляла 2400 квадратных метров.Какими должны быть размеры поля?
Решение Здесь задействованы две формулы. P = 2l + 2w для периметра и A = lw для площади.
Сначала используя P = 2l + 2w, получаем
Теперь мы можем использовать формулу A = lw и подставить (100 — l) вместо w, получив
Поле должно быть шириной 40 метров и длиной 60 метров.
| Мы могли бы точно так же решить для l, получив l = 100 — w. Тогда |
Обратите внимание, что в этой задаче мы фактически используем систему уравнений
P = 2 l + 2 w
A = l w.


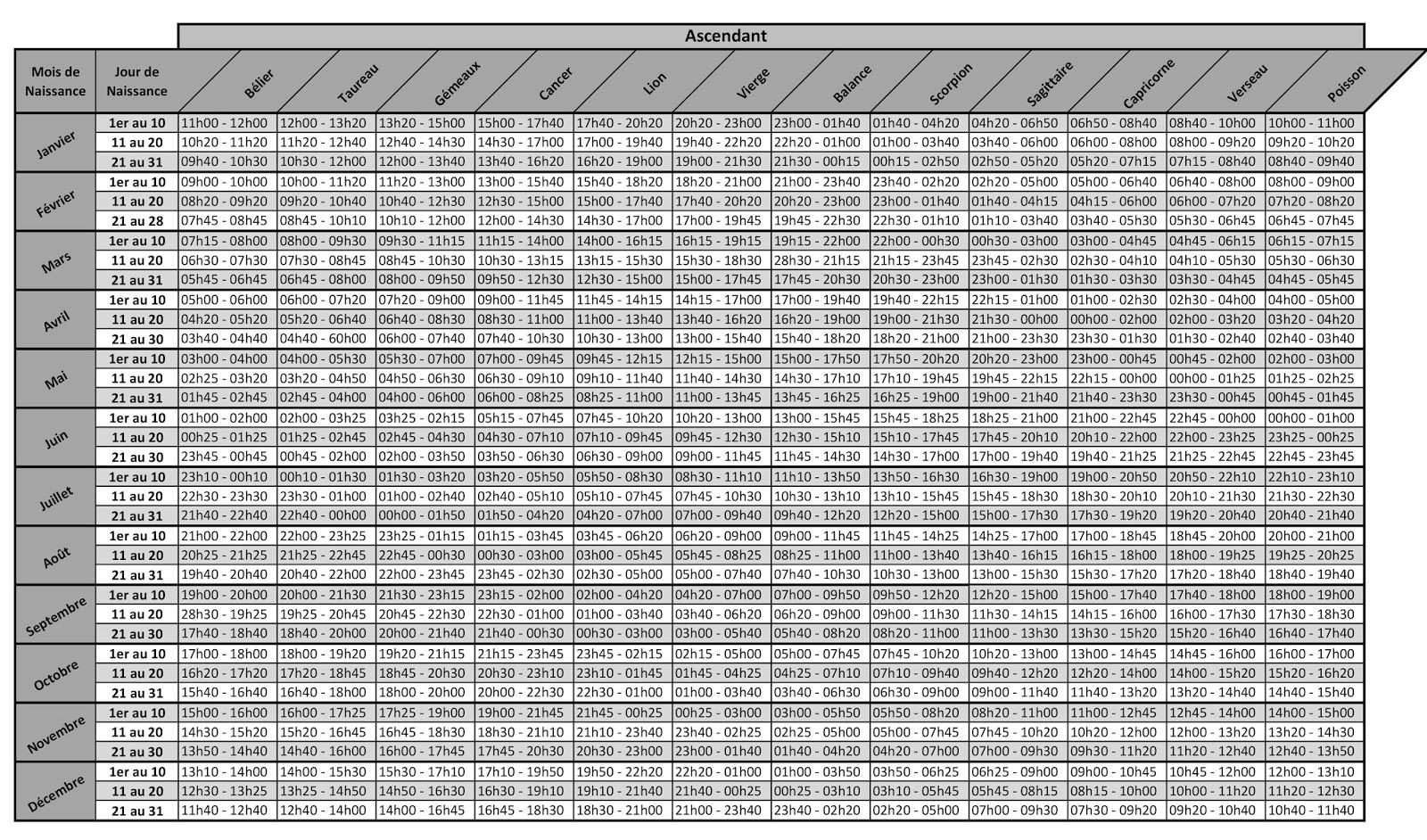
 Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]
Чтобы получить «а» нужно всего лишь
разделите коэффициент x на 2. Таким образом, чтобы построить квадрат для x 2 + 2ax, нужно добавить 2 .]