Какое число скрыто под парковочным местом – Номер парковочного места. Логическая задача

пять детских головоломок, которые вводят в ступор взрослых — Офтоп на TJ

Кадр из фильма «Игры разума»

Номер парковочного места

Задачка для гонконгских школьников, которая набрала «вирусную» популярность в середине 2014 года. На её решение у шестилетнего ребёнка обычно уходит не больше 20 секунд, а вот неподготовленных взрослых она часто вводит в ступор.

Какое число скрыто под машиной?

Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.

Другая математика

Известная задача, которую дошкольники решают за 5-10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.

Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.

У этой задачи есть хороший аналог:

1 = 5

2 = 25

3 = 125

4 = 625

5 = ?

Ханна и резко повышенная сложность

Знаменитая задачка-мем, в которой итоговый вопрос кажется куда более сложным, чем условие.

В сумке n конфет. Шесть из них оранжевые. Остальные — жёлтые. Ханна берёт конфету из сумки и съедает. Затем берёт ещё одну и снова съедает. Вероятность того, что она съела две оранжевые конфеты —

1/3. Докажите, что n²–n–90=0.

Странное завершение истории Ханны породило в сети множество шуток. Самая известная: «Ханна съела несколько конфет. Рассчитайте длину окружности экватора Юпитера с помощью кальки и ржавой ложки».

Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить n, однако в действительности этого не требуется.

Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.

Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.

Куда едет автобус

Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?

Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.

Для терпеливых

Ещё одна «вирусная» задачка. Как сообщает The Guardian, вьетнамский учитель даёт её восьмилетним детям, и они справляются. При этом решения за короткое время не смогли дать даже люди с докторской степенью по экономике и математике.

Нужно заполнить пустые клетки числами от 1 до 9, так чтобы выражение было верным.

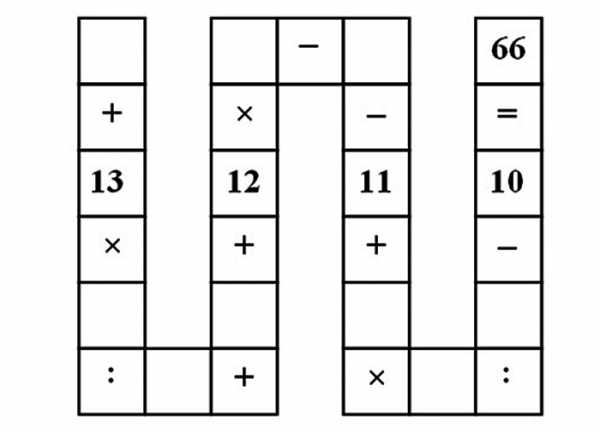Решение: с помощью этой задачки детей учат запоминать порядок, в котором производятся действия сложения, вычитания, умножения и деления. К сожалению, в данном случае у проблемы нет какого-то изящного и быстрого решения.

Начать следует, записав таблицу в виде уравнения:

a + (13⋅b/c) + d + 12⋅e – f – 11 + (g⋅h/i)– 10 = 66

А затем привести его к виду:

a + d – f + (13⋅b/c) + 12⋅e +(g⋅h/i) = 87

Можно предположить, что b/c и gh/i должны быть целыми, а 13⋅b/c не должно быть слишком большим. На этом этапе многие предпочитают написать программу, однако при желании можно просто перебрать около сотни вариантов.

Дети обычно решают, что для минимизации 13⋅b/c, b должно быть равно 2, а c — 1.

Получаем:

a + d – f + 12e +(gh/i) = 61

Затем дети понимают, что им необходимо быстрее избавиться от 3,5 и 7, вызывающих сложности при делении, и присваивают эти значения

a, d и f соответственно.

Итог: 12e +(gh/i) = 60

Немного поигравшись с оставшимися цифрами, можно выяснить, что e=4, g=9, h=8, i=6.

Таким образом дети решают эту задачку, если всегда идут по самому простому пути, а взрослые, ищущие от жизни подвоха, с ней зачастую не справляются.

С ответами всё очень и очень просто,
Вадим Елистратов,
TJ

tjournal.ru

Пять детских головоломок, которые вводят в ступор взрослых

Фактрум публикует пять известных задач, которые поразительно легко даются детям.

Номер парковочного места

Задачка для гонконгских школьников, которая набрала «вирусную» популярность в середине 2014 года. На её решение у шестилетнего ребёнка обычно уходит не больше 20 секунд, а вот неподготовленных взрослых она часто вводит в ступор.

Какое число скрыто под машиной?

Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.

Другая математика

Известная задача, которую дошкольники решают за 5–10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.

Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.

У этой задачи есть хороший аналог:

1 = 5
2 = 25
3 = 125
4 = 625
5 = ?

Ханна и резко повышенная сложность

Знаменитая задачка-мем, в которой итоговый вопрос кажется куда более сложным, чем условие.

В сумке n конфет. Шесть из них оранжевые. Остальные — жёлтые. Ханна берёт конфету из сумки и съедает. Затем берёт ещё одну и снова съедает. Вероятность того, что она съела две оранжевые конфеты — 1/3. Докажите, что n²-n-90=0.

Странное завершение истории Ханны породило в сети множество шуток. Самая известная: «Ханна съела несколько конфет. Рассчитайте длину окружности экватора Юпитера с помощью кальки и ржавой ложки».

Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить n, однако в действительности этого не требуется.

Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.

Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.

Куда едет автобус

Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?

Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.

Для терпеливых

Ещё одна «вирусная» задачка. Как сообщает The Guardian, вьетнамский учитель даёт её восьмилетним детям, и они справляются. При этом решения за короткое время не смогли дать даже люди с докторской степенью по экономике и математике.

Нужно заполнить пустые клетки числами от 1 до 9, так чтобы выражение было верным.

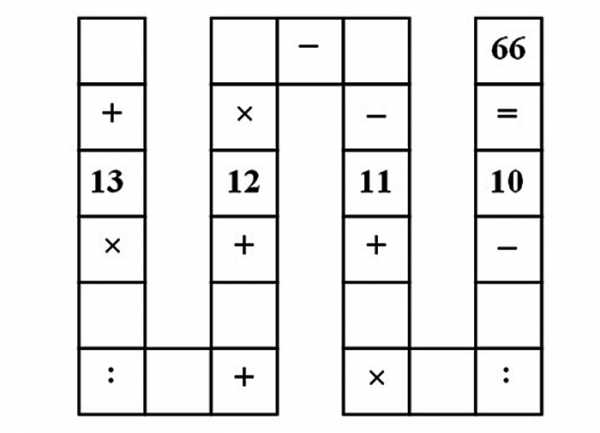
Решение: с помощью этой задачки детей учат запоминать порядок, в котором производятся действия сложения, вычитания, умножения и деления. К сожалению, в данном случае у проблемы нет какого-то изящного и быстрого решения.

Начать следует, записав таблицу в виде уравнения:

a + (13⋅b/c) + d + 12⋅e — f — 11 + (g⋅h/i)- 10 = 66

А затем привести его к виду:

a + d — f + (13⋅b/c) + 12⋅e +(g⋅h/i) = 87

Можно предположить, что b/c и gh/i должны быть целыми, а 13⋅b/c не должно быть слишком большим. На этом этапе многие предпочитают написать программу, однако при желании можно просто перебрать около сотни вариантов.

Дети обычно решают, что для минимизации 13⋅b/c, b должно быть равно 2, а c — 1.

Получаем:

a + d — f + 12e +(gh/i) = 61

Затем дети понимают, что им необходимо быстрее избавиться от 3,5 и 7, вызывающих сложности при делении, и присваивают эти значения a, d и f соответственно.

Итог: 12e +(gh/i) = 60

Немного поигравшись с оставшимися цифрами, можно выяснить, что e=4, g=9, h=8, i=6.

Таким образом дети решают эту задачку, если всегда идут по самому простому пути, а взрослые, ищущие от жизни подвоха, с ней зачастую не справляются.

Читайте также: Головоломка для 14-летних, которую не может решить весь интернет

Александр Таранов04.11.2015

www.factroom.ru

ПЯТЬ ДЕТСКИХ задачек, которые вводят в ступор взрослых

Говорят, что  на решение этих задач у маленьких детей уходит всего по 5–10 минут, а взрослые тратят на них часы, а нередко и вообще не могут с ними справиться!

Давайте попробуем и мы, а потом отметимся в опросе  …

Какие задачки вы решили без подсказки?

1. Номер парковочного места

Задачка для гонконгских школьников, которая набрала «вирусную» популярность в середине 2014 года. На её решение у шестилетнего ребёнка обычно уходит не больше 20 секунд, а вот неподготовленных взрослых она часто вводит в ступор.

Какое число скрыто под машиной?

[РЕШЕНИЕ]Решение: как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.

2. Другая математика

Известная задача, которую дошкольники решают за 5–10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.

[РЕШЕНИЕ]

Решение: маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.

У этой задачи есть хороший аналог:

1 = 5
2 = 25
3 = 125
4 = 625
5 = ?

3. Ханна и резко повышенная сложность

Знаменитая задачка-мем, в которой итоговый вопрос кажется куда более сложным, чем условие.

В сумке n конфет. Шесть из них оранжевые. Остальные — жёлтые. Ханна берёт конфету из сумки и съедает. Затем берёт ещё одну и снова съедает. Вероятность того, что она съела две оранжевые конфеты — 1/3. Докажите, что n²-n-90=0.

Странное завершение истории Ханны породило в сети множество шуток. Самая известная: «Ханна съела несколько конфет. Рассчитайте длину окружности экватора Юпитера с помощью кальки и ржавой ложки».

[РЕШЕНИЕ]Решение: многие пользователи сети никак не могут найти решение, потому что убеждены, что для него нужно сначала вычислить n, однако в действительности этого не требуется.

Вероятность того, что в первый раз Ханна вытянула оранжевую конфету — 6/n (в сумке шесть оранжевых из n конфет). Если в первый раз Ханна вытянула оранжевую конфету, то вероятность вытянуть такую же во второй раз — 5/(n-1). Вероятность вытянуть две оранжевые конфеты — произведение этих двух вероятностей.

Получаем: (6/n)⋅(5/(n-1))=¹⁄₃. Дальше достаточно упростить уравнение.

4. Куда едет автобус

Издевательски простая задача, которая попадает во все сборники такого рода головоломок — понятных детям и непонятных взрослым. Куда едет автобус?

[РЕШЕНИЕ]Решение: обычно взрослые, видя схематичное изображение, мигом забывают о деталях. В США дети часто ездят в школу на автобусе, поэтому знают, с какой стороны у него двери и как он подъезжает. Они понимают, что на картинке не хватает дверей. Значит, автобус едет влево. Само собой, вариант, что он сдаёт назад, не рассматривается.

5. Для терпеливых

Ещё одна «вирусная» задачка. Как сообщает The Guardian, вьетнамский учитель даёт её восьмилетним детям, и они справляются. При этом решения за короткое время не смогли дать даже люди с докторской степенью по экономике и математике.

Нужно заполнить пустые клетки числами от 1 до 9, так чтобы выражение было верным.

[РЕШЕНИЕ]Решение: с помощью этой задачки детей учат запоминать порядок, в котором производятся действия сложения, вычитания, умножения и деления. К сожалению, в данном случае у проблемы нет какого-то изящного и быстрого решения.

Начать следует, записав таблицу в виде уравнения:

a + (13⋅b/c) + d + 12⋅e — f — 11 + (g⋅h/i)- 10 = 66

А затем привести его к виду:

a + d — f + (13⋅b/c) + 12⋅e +(g⋅h/i) = 87

Можно предположить, что b/c и gh/i должны быть целыми, а 13⋅b/c не должно быть слишком большим. На этом этапе многие предпочитают написать программу, однако при желании можно просто перебрать около сотни вариантов.

Дети обычно решают, что для минимизации 13⋅b/c, b должно быть равно 2, а c — 1.

Получаем:

a + d — f + 12e +(gh/i) = 61

Затем дети понимают, что им необходимо быстрее избавиться от 3,5 и 7, вызывающих сложности при делении, и присваивают эти значения a, d и f соответственно.

Итог: 12e +(gh/i) = 60

Немного поигравшись с оставшимися цифрами, можно выяснить, что e=4, g=9, h=8, i=6.

Таким образом дети решают эту задачку, если всегда идут по самому простому пути, а взрослые, ищущие от жизни подвоха, с ней зачастую не справляются.

А вот несколько умнейших в мире детей.

АКРИТ ЙАСУАЛ (AKRIT JASWAL)

Этот индийский мальчонка стал самым молодым врачом в мире. Пяти лет от роду он уже прекрасно ориентировался в анатомии и читал Шекспира, а в семь лет провёл свою первую хирургическую операцию! Дело было так: доктора в местной больнице заметили, что ребенок активно интересуется медициной, и позволили ему наблюдать за операциями. Акрит прочел все, что мог, о предмете и своими комментариями убедил профессионалов, что действительно разбирается в хирургии. Когда ему было семь, бедная семья попросила его провести операцию их дочери, потому что они не могли заплатить настоящему врачу. Все прошло успешно.

Он обладает наивысшим IQ среди соотечественников (146 пунктов). В настоящее время подросток Акрит — самый молодой студент медицинского университета

ПАБЛО ПИКАССО (PABLO PICASSO)

Рисовать Пабло начал раньше, чем научился говорить. Как гласит легенда, он сам жестами попросил своего отца вложить ему в руку кисть и научить азам рисования.

Хотя другие школьные предметы давались ему с трудом, а систему счёта он, кажется, так и не осилил до конца долгой жизни. К 12 годам он настолько мастерски и реалистично воспроизводил натуру на холсте, что считался уже зрелым художником со своим неповторимым почерком, в то же время читая по слогам и допуская многочисленные орфографические ошибки при письме. Но экзамены в Школу искусств подросток сдал блестяще за один день, хотя обычно у начинающих художников на это уходил целый месяц. В 16 лет состоялась его первая выставка, а в 20 он был всемирно знаменитым.

ГОВАРД ФИЛЛИПС ЛАВКРАФТ (HOWARD PHILLIPS LOVECRAFT)

Праотец всей мистической литературы, создатель истории о Ктулху, Лавкрафт овладел чтением в два года, а в шесть уже писал сложные серьёзные стихотворные произведения. Угрюмый и болезненный мальчик с детства увлёкся созданием собственной пугающей вселенной с населяющими её ужасными существами.

Ужасы он переносил на бумагу из своих детских снов: да, вот такие мальчику снились кошмары. Во многом всему этому способствовала домашняя обстановка.

Его отца упрятали в сумасшедший дом с диагнозом «необратимые психические изменения, вызванные сифилисом», когда Говарду было три года. Мать, вечно подавленная, хилая и белая как смерть женщина, также закончила свои дни в психлечебнице. Юный Лавкрафт переболел всеми возможными болезнями и подолгу оставался в постели, слушая страшные сказки из уст своего эксцентричного дедушки Уиппла, обладателя самой большой библиотеки в городке. Говард с детства был поразительно увлечённым человеком, интересующимся не только литературой, но и астрономией, историей, химией.

ВОЛЬФГАНГ АМАДЕЙ МОЦАРТ (WOLFGANG THEOPHILUS MOZART)

Моцарт не только один из величайших композиторов всех времен, но и, пожалуй, наиболее известный вундеркинд во всей мировой истории.

В четыре года он уже виртуозно играл на фортепиано, а в пять написал свои первые небольшие музыкальные пьесы. В возрасте восьми лет, когда обычные дети не отличают контрабас от виолончели — если вообще понимают, что означают эти слова — Моцарт закончил написание своей первой симфонии.

ОКИТА СОДЗИ (OKITA SOJI)

Этот японский вундеркинд немного из другой области, нежели вышеперечисленные. Он жил в середине 19 века и не отличался выдающимися интеллектуальными способностями. Зато никто не мог его победить.

В возрасте девяти лет, когда многим детям ещё не дают пользоваться столовыми ножами, чтоб не порезались, он в совершенстве овладел боевыми саблями и мечами (бокеной, катаной, синаем). В 12 лет он с лёгкостью победил знаменитого мастера фехтования. Официально стал признанным мастером боевых искусств в 18 лет. Окита был одним из организаторов прославленной военной полиции Синсэнгуми, легенды о которой популярны в Японии по сей день, воплощённые в комиксах, фильмах и видеоиграх.

КИМ УНГ ЙОНГ (KIM UNG-YONG)

Согласно книге рекордов Гиннеса, кореец Ким Унг Йонг до сих пор считается самым умным из ныне живущих людей и имеет наивысший IQ — 210 пунктов! Ким стал студентом физического факультета университета, когда ему было всего три года, и блестяще его закончил в шесть. Позже, будучи уже «зрелым» семилеткой, он был приглашён в США на работу в НАСА. (Может, в НАСА подозревали, что он инопланетянин, и хотели его исследовать?) Тем не менее, в 15 лет он уже имел докторскую степень и невероятные перспективы.

Правда, повзрослев, Ким решил вернуться на родину в Корею и преподавать в обычном высшем учебном заведении провинциального городка.

ГРЕГОРИ СМИТ (GREGORY SMYTH)

Грегори Смит родился в 1990 году в США и в 2 года уже умел читать, а в 10 начал обучение на первом курсе университета. Понятно, что на фоне таких феноменов, как кореец Ким Унг Йонг, достижения подростка Грегори выглядят бледновато и вряд ли кого могут удивить.

Так что же такого особенного есть у паренька Грегори Смита, что даёт ему право занять почётное место в списке выдающихся вундеркиндов?

Дело в том, что, как показывают исследования, большинство одарённых детишек, мягко говоря, странноватые. Они или «ботаны», или социопаты, или и то, и другое. А Грег Смит отнюдь не таков! Паренёк смекнул, что ниша молодых политиков до сих пор свободна, и основал детское общественное движение «для достижения понимания между детьми всего мира». Как глава этого достойного движения одарённый молодец удосужился аудиенции с Михаилом Горбачёвым и Биллом Клинтоном, а затем произнёс зажигательный спич с трибуны ООН. На гребне популярности его четырежды номинировали на получение Нобелевской премии мира.

УИЛЬЯМ ДЖЕЙМС САЙДИС (WILLIAM JAMES SIDIS)

Некоторые считают Уильяма Сайдиса самым умным человеком, когда-либо жившим на Земле. Его уровень IQ по самым скромным подсчётам колебался между 250-300 пунктами. Для сравнения: если ваш коэффициент интеллекта равен 136 пунктам, можете смело причислять себя к гениям. Интеллект обычного человека со средними способностями колеблется в пределах от 85 до 115 пунктов.

Рождённый в США в 1898 году, сын эмигрантов из России, Сайдис научился читать в полтора года, а к восьми написал уже четыре книги и владел семью иностранными языками: латынь, греческий, русский, иврит, французский, немецкий. А седьмой — Vendergood — мальчик придумал сам на основе греческого, латыни и современных языков романо-германской группы. В семь лет сдал экзамен Гарвардской медицинской школы по анатомии, и его не приняли в университет только из-за возраста. В 11 лет его отец добился зачисления в Гарвард. Уильям стал профессором, еще не достигнув 20 лет. Несмотря на его потрясающие работы по математике и космологии, даже родители начали сомневаться в его адекватности после того, как в половозрелом возрасте он заявил, что осознанно принял целибат, то есть отказался от отношений с противоположным полом. Уильям Сайдис так и умер девственником.

Он вел затворнический образ жизни, переезжая из города в город и меняя работу, чтобы скрыть от окружающих свою гениальность.

Микаэла Фудолиг

Микаэла Ирэн Фудолиг поступила в Филиппинский университет в 11 лет, а в 16 лет она окончила его с отличием, получив степень бакалавра физических наук — она стала выпускником, произносящим прощальную речь. В настоящее время Микаэла работает профессором в том же университете и занимается эконофизикой — математическим моделированием поведения в системах и биологическими системами.

Тейлор Уилсон

Тейлор Рамон Уилсон стал самым молодым человеком в мире, создавшим рабочий фузор — устройство, предназначенное для реакций ядерного синтеза. В возрасте 10-ти лет он сконструировал ядерную бомбу, а фузор сделал, когда ему исполнилось 14. В мае 2011-го года Тейлор получил премию на Международной научно-технической ярмарке Intel за детектор переходного излучения.

В феврале 2013-го года он выступил на конференции TED-2013, где рассказал о своих идеях относительно автономных подземных ядерных реакторов деления. Тейлор разработал компактный ядерный реактор, который, по его словам, способен генерировать 50 МВт электроэнергии, причём заправлять устройство необходимо только раз в 30 лет.

Камерон Томпсон

Камерон Томпсон — математический гений из Северного Уэльса. Когда ему было четыре года, он поправил своего учителя, сказавшего, что нуль является наименьшим числом, заявив, что тот забыл об отрицательных числах. В возрасте 11-ти лет он получил степень по математике в Открытом университете Великобритании. В том же возрасте мальчик успешно сдал два выпускных экзамена в математической школе и был показан по ВВС как один из гениальных подростков. К сожалению, у Камерона есть трудности в учёбе из-за болезни Аспергера, но, тем не менее, он является одним из юных математических гениев в мире.

Джейкоб Барнетт

Джейкоб Барнетт — американский математик. Когда ему было два года, ему поставили диагноз — тяжёлый аутизм: врачи говорили, что тот не сможет говорить, читать и совершать мелкие бытовые действия. В три года оказалось, что врачи крупно ошиблись — Джейкоб мог рассказать алфавит в прямом и обратном порядке.

В этом же возрасте во время посещения планетария Джейкоб ответил на вопрос ведущего о том, почему луны Марса такой странной формы. Он поступил в Университет Индианы в Индианаполисе в возрасте 10-ти лет.

Во время работы над своей докторской диссертацией Барнетт утверждал, что в один прекрасный день сможет опровергнуть теорию относительности Эйнштейна. В настоящее время он работает над диссертацией в области квантовой физики.

Марк Тянь Боэдихарджо

Марк Тянь Боэдихарджо родился в Гонконге, он — самый молодой человек, поступивший в Гонконгский университет: ему тогда было девять лет. Он учился по специальной программе, где особое внимание уделялось математике и статистике, в то же время он сдал в школе восемь выпускных экзаменов.

Сейчас у Марка есть два диплома, степень бакалавра в области математических наук и магистра философии в области математики, которую он получил в 2011-м году — на год раньше, чем предусматривает учебный план. В настоящее время он получает степень доктора философии математики в Соединенных Штатах.

Приянши Сомани

Приянши Сомани из Индии обладает удивительной способностью проводить в уме сложнейшие математические вычисления. В шесть лет она освоила устный счёт, а в 11 заняла первое место на соревновании «Mental Calculation World Cup»: Приянши обошла 36 других конкурентов из 16-ти стран, вычислив квадратный корень из десяти шестизначных чисел за рекордные 6 минут и 51 секунду. В довершение всего, она оказалась единственным участником в истории конкурса, не допустившим ни одной ошибки при сложении, умножении и извлечении квадратных корней.

Приянши стала новым мировым рекордсменом в извлечении квадратных корней в уме в январе 2012-го года, когда вычислила квадратный корень из десяти шестизначных чисел за 2 минуты и 43 секунды.

Аким Камара

Аким Камара — скрипач из Берлина. Он начал играть на скрипке в два года и отличается замечательной памятью о музыке, которую слышал ещё в пеленках. Его учитель заметил его естественный «музыкальный слух» и начал преподавать мальчику уроки музыки дважды в неделю. Играть на скрипке Аким научился исключительно быстро, всего за шесть месяцев обучения, и дебютировал в декабре 2003-го года в возрасте трёх лет на рождественском концерте.

Итан Бортник

Итан Бортник — музыкант, автор песен и актёр. Когда ему было три года, он начал играть на клавесине, а в возрасте пяти лет — писать музыку. Его дебютное выступление состоялось на «The Tonight Show» с Джеем Лено в 2007-м году, после чего мальчик неоднократно выступал в дальнейшем.

Итан вошёл в Книгу Рекордов Гиннеса как самый молодой сольный исполнитель в мире. Он также является самым молодым хедлайнером, который когда-либо выступал в Лас-Вегасе — концерт состоялся, когда Итану было десять лет.

Таниш Мэттью Авраам

Таниш Мэттью Авраам — один из самых молодых членов Менса, куда он вступил в возрасте четырёх лет. Его гениальность проявилась в четыре месяца, когда тот стал просматривать детские книги и правильно отвечать на вопросы об их содержании.

При вступлении в Менса он получил результат в 99,9% по стандартизированному тесту IQ Менса. В пять лет Таниш закончил пять курсов математики образовательной программы Стэндфордского университета для одаренной молодёжи всего за шесть месяцев.

В шесть лет он поступил в среднюю школу, а затем в колледж — по всем предметам его средний бал никогда не опускался ниже 4.0. Также он часто публикует эссе на вебсайте Лунного института НАСА.

Не смог найти достаточной информации о российских детях вундеркиндах. Кто подскажет примеры в комментах ?

Вот вам еще Задачка с шариками и водой, а вот еще Простая логическая загадка. Могу еще вот такую задачку подсказать с собачками и задачка в какую сторону поедет велосипед

masterok.livejournal.com

4 детских задачки, которые вводят в ступор взрослых

Post Views: 278

В это трудно поверить, но на решение этих задач у маленьких детей уходит всего по несколько минут, а взрослые тратят на них часы, а нередко и вообще не могут с ними справиться! Как вы думаете, в чём тут дело?

Какое число скрыто под машиной?

Решение: 

Спойлер

как часто бывает в подобных случаях, проблема взрослых заключается в том, что они идут слишком сложным путём — например, пытаются высчитать закономерность, согласно которой расположены номера парковочных мест. В действительности же картинку надо просто мысленно перевернуть.

[свернуть]

Другая математика

Известная задача, которую дошкольники решают за 5–10 минут. У некоторых программистов уходит на неё до часа, а многие люди, исписав несколько листов бумаги, сдаются.

Решение: 

Спойлер

маленькие дети не могут составлять уравнения или искать математические закономерности, поэтому они замечают, что значение зависит от количества кружочков в каждой цифре. В 9 один кружочек, в 8 — два, в 1 — ни одного, а, значит, 2581=2.

[свернуть]

Куда едет автобус

naoblake.com

Парковка — Задачи — Парковка — Задачи

Парковка имеет n мест, пронумерованных от 1 до n включительно. Парковка открывается пустой каждое утро и работает на протяжении дня следующим образом. Когда автомобиль приезжает на парковку, парковщик проверяет, есть ли свободные места. Если таковых нет, автомобиль ожидает возле въезда до тех пор, пока освободится какое-то место. Если есть свободное место, или как только оно освобождается, автомобиль занимает свободное парковочное место. Если есть несколько свободных парковочных мест, автомобиль занимает место с наименьшим номером. Когда приезжают парковаться другие автомобили, но уже есть ожидающий автомобиль, они выстраиваются в очередь на въезде в том порядке, в котором приехали. После того, как освобождается парковочное место, его занимает первый автомобиль из очереди (то есть тот, который прибыл парковаться первым).

Стоимость парковки одного автомобиля в долларах определяется как произведение веса этого автомобиля в килограммах на тариф его парковочного места. Стоимость парковки автомобиля не зависит от того, сколько времени этот автомобиль находится на парковке.

Парковщик знает, что сегодня на парковку приедет m автомобилей, и он знает порядок их приезда и отъезда. Помогите ему подсчитать, сколько долларов он сегодня заработает.

Напишите программу, которая по заданным тарифам парковочных мест, весам автомобилей и порядку, в котором автомобили приезжают и уезжают, определяет доход парковки в долларах.

Входные данные

Первая строка содержит два целых числа — количество парковочных мест n (1 ≤ n ≤ 100) и количество автомобилей m (1 ≤ m ≤ 2,000), разделенные пробелом.

Следующие n строк описывают тарифы парковочных мест, s-ая из этих строк содержит одно целое число r_s (1 ≤ r_s ≤ 100) – тариф парковочного места с номером s в долларах за килограмм.

Следующие m строк описывают веса автомобилей. Автомобили пронумерованы в произвольном порядке от 1 до m включительно, k-ая из этих m строк содержит одно целое число w_k (1 ≤ w_k ≤ 10,000) – вес автомобиля с номером k в килограммах.

Следующие 2m строк описывают приезд и выезд всех автомобилей в хронологическом порядке. Положительное целое число i показывает, что автомобиль с номером i приезжает на парковку. Отрицательное целое число —i показывает, что автомобиль с номером i уезжает с парковки. Никакой автомобиль не выезжает с парковки до своего приезда, и все автомобили от 1 до m включительно появятся в этой последовательности строк ровно 2 раза, один раз как приезжающий, и второй – как выезжающий. К тому же, никакой из автомобилей не выедет с парковки, пока не займет место на парковке (то есть, никакой автомобиль не уедет пока стоит в очереди).

Выходные данные

Одно целое число — общее количество долларов, которое заработает сегодня парковщик.

Лимит времени 1 секунда

Лимит использования памяти 64 MiB

 Источник IOI-2009, Day 2

www.e-olymp.com